Problema nº 5 de capacitores o condensadores, energía y capacidad en un capacitor - TP06

Enunciado del ejercicio nº 5

Un capacitor plano posee una capacidad de 200 µF y la distancia entre sus placas es de 0,6 mm. Si cuando se carga adquiere un potencial de 600 V. ¿Cuál es la energía almacenada y cuál sería la capacidad si la distancia entre sus placas se lleva a 3 mm?

Desarrollo

Datos:

C = 200 µF = 0,0002 F

s₁ = 0,6 mm = 0,0006 m

V = 600 V

s₂ = 3 mm = 0,003 m

Fórmulas:

U = ½·C·V²

Solución

Calculamos la energía del capacitor.

U = ½·C·V²

Reemplazamos por los valores y calculamos:

U = ½·0,0002 F·(600 V)²

U = 0,0001 F·360.000 V²

Resultado, la energía del capacitor es:

U = 36 J

Calculamos la capacidad.

Empleamos la fórmula de capacidad para ambos casos:

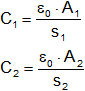
El área del capacitor no varía y el medio es el mismo:

A₁ = A₂ = A

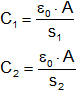
Despejamos "ε₀·A" e igualamos:

C₁·s₁ = C₂·s₂

Despejamos "C₂":

Reemplazamos por los valores y calculamos:

Resultado, la capacidad que posee para una distancia de 3 mm es:

C₂ = 0,00004 F

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP06
• | Siguiente ›

Ejemplo, cómo determinar la energía y la capacidad en un capacitor