Densidad de campo eléctrico
En electrostática, las líneas de fuerza son siempre perpendiculares a la superficie; no así en electrodinámica.
![]()
![]()
σ: densidad de campo eléctrico.
A: área.
![]()
![]()
![]()
![]()
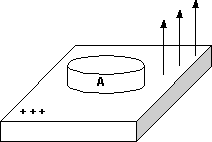
Líneas de fuerza del campo eléctrico
Carga de un electrón
Experimento de Robert Andrews Millikan: el objeto es que la gota cargada electrostáticamente, permanezca suspendida por el equilibrio entre el campo eléctrico y el campo gravitatorio. Para lograr el equilibrio de los campos:
E·q = m·g
![]()
Como:
![]()
![]()
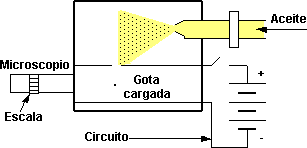
Esquema del experimento de Robert Andrews Millikan
La velocidad de caída de la gota es constante debido a la fricción del aire, según la Ley de Stock:
Ff = 6·π·η·a·vₜ ⟶ Fuerza de fricción
P = m·g = Vgota·Δaceite·g = 4·π·a³·Δaceite·g/3 ⟶ Fuerza peso de la gota.
Fb = 4·π·a³·Δaire·g/3 ⟶ Fuerza de empuje
Luego:
Ff + Fb = P
6·π·η·a·vₜ + 4·π·a³·Δaceite·g/3 = 4·π·a³·Δaire·g/3
Finalmente la carga del electrón es:
qₑ = 1,60·10⁻¹⁹ C
Otra forma de interpretar la diferencia de potencial
Si F es gravitatoria:
![]() ⟶ k* = G·m₁·m₂
⟶ k* = G·m₁·m₂
Si F es eléctrica:
k* = G·m₁·m₂
Ejemplo:
Se quiere mover una carga Q desde "b" hasta "a".
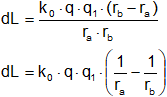
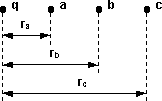
Ejemplo de diferencia de potencial
![]()
En el infinito 1/r ⟶ 0, por lo tanto, se desprecia.
![]()
Como:
![]()
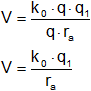
Si un campo está colocado a un metro de una carga de 1 C/9·10⁹, entonces:
![]()
V = 1 N·m/C
Capacitancia
La capacidad de un condensador se mide en faradio: un condensador de 1 F tiene una diferencia de potencial entre sus placas de 1 V cuando éstas presentan una carga de 1 C.
![]()
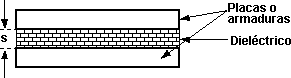
Esquema de un condensador
![]()
C: capacidad.
Sabemos que:
![]() ∧
∧ ![]()
V = E·s
![]()
![]()
![]()
A: superficie de las placas.
s: distancia entre las placas.
ε₀ = 8,854185·10⁻¹² C²/N·m² (permeabilidad del vacío).
Dieléctrico
La mayor parte de los capacitores tienen entre sus placas un material sólido no conductor o dieléctrico.
La capacitancia de un capacitor es mayor cuando hay un dieléctrico entre las placas que cuando éstas están separadas únicamente por el aire o el vacío.
![]()
C: capacidad con dieléctrico entre las placas.
C₀: capacidad con vacío entre las placas.
εᵣ: constante dieléctrica del material colocado entre las placas.
Ver tabla de constantes dieléctricas
Energía en un capacitor
El trabajo necesario para cargar un capacitor desde 0 hasta "V":
L = ½·q·V
Como:
![]()
q = C·V
Reemplazando:
L = ½·C·V·V
L = U = ½·C·V²
Circuitos con capacitores
Capacitores en paralelo.
qT = q₁ + q₂ + q₃
q = C·V
C·V = C₁·V₁ + C₂·V₂ + C₃·V₃
Pero:
V = V₁ = V₂ = V₃
C·V = C₁·V + C₂·V + C₃·V
C·V = (C₁ + C₂ + C₃)·V
C = C₁ + C₂ + C₃
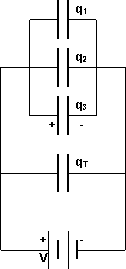
Circuito de capacitores en paralelo
Capacitores en serie.
V = V₁ + V₂ + V₃
![]()
![]()
Pero:
qT = q₁ = q₂ = q₃
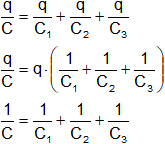
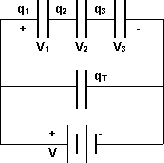
Circuito de capacitores en serie
Autor: Ricardo Santiago Netto. Argentina
¿Cuál es la carga de un electrón?