Principio de superposición - Teorema de Coulomb

Campo en un punto infinitamente próximo a un conductor cargado y en equilibrio. Teorema de Coulomb

E =	σ
	ε

"El campo en un punto infinitamente próximo es igual a σ entre la constante dielectrica (ε) del medio que envuelve al conductor".

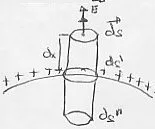
Esquema de un campo en un punto infinitamente próximo a un conductor cargado y en equilibrio

Colocamos sobre la superficie ds' una superficie gaussiana, un cilindro.
Φ = (ds") = 0. Está en el interior del conductor.
Φ = (lateral) = 0. No atraviesan las líneas de fuerza lateralmente al cilindro.

Solo hay Φ por ds.

E·ds =	dq
	ε

E =	dq
	ε·ds

E =	σ
	ε

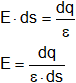
Por definición de flujo:

dΦ = Ē·ds = E·ds·cos α = E·ds

Por Teorema Gauss:

dΦ =	dq
	ε

Esto ocurre siempre que E es perpendicular a dS'

Esto sirve para un condensador plano

Líneas paralelas de campo perpendiculares a la superficie

Líneas paralelas E = constante.
En los terminales el campo se curva pero suele despreciarse.

Campo creado por un plano infinito cargado uniformemente

Campo creado por una distribución esférica de carga en el exterior

El plano cargado se caracteriza por su densidad superficial de carga constante σ = Q/S
Por simetría, las líneas de campo son paralelas entre sí y perpendiculares al plano
Elegimos como superficie de Gauss, S_G, un paralelepípedo perpendicular al plano
Calculamos el flujo eléctrico a traves de S_G. Sólo contribuyen al flujo eléctrico las caras paralelas al plano: S₁ y S₂. El flujo a traves de las otras caras es nulo porque Ē y dS son perpendiculares

Φ = ∫_SG Ē·dS = ∫_S1 E·dS + ∫_S2 E·dS

Φ = E·S₁ + E·S₂ = 2·E·S

Aplicamos el teorema de Gauss:

Φ =	Q
	ε₀

2·E·S =	Q
	ε₀

E =	Q
	2·ε₀·S

E =	σ
	2·ε₀

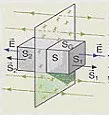
Esquema de un campo creado por un plano infinito cargado uniformemente

El campo eléctrico creado por un plano infinito de carga es uniforme.

La esfera, de radio R, tiene una carga Q distribuida uniformemente
Por simetría, el campo es radial y sólo depende de la distancia r al centro de la esfera
Elegimos como superficie de Gauss S_G una esfera concéntrica con la distribución de carga, de radio r > R
Calculamos el flujo eléctrico a traves de S_G. Sobre la superficie de Gauss el campo eléctrico Ē tiene módulo constante y dirección paralela a dS
Φ = ∫_SG Ē·dS = ∫_S1 E·dS = E·S_G = E·4·π·r²
Aplicamos el teorema de Gauss:

Φ =	Q
	ε₀

E·4·π·r² =	Q
	ε₀

E =	1	·	Q
	4·π·ε₀		r²

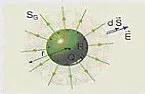
Esquema de un campo creado por una distribución esférica de carga en el exterior

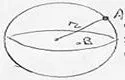
El campo eléctrico creado por una distribución esférica de carga en un punto exterior es el mismo que crearía una carga puntual Q situada en el centro de la esfera.

Potencial creado por una esfera uniformente cargada en el exterior

dW = F·dř = q·Ē·dR = q·E·dR	E·dR = V₁ - V₂
dW = -ΔEₚ = (V₁ - V₂)·q

V = ∫	∞	·E·dr

	R

El punto 2 me lo llevo al ∞.

V = ∫	∞	·E·dr

	R

V = ∫	∞	1 4·π·ε	·	q R²	·dr

	R

V =	1 4·π·ε	·Q·[	-1 R	]	∞

					R

V =	1	·	Q
	4·π·ε		r

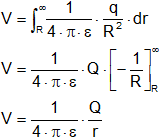
El potencial creado por la esfera es como si la carga estuviera en el centro de la esfera.

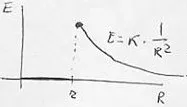
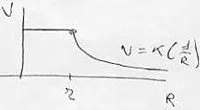
En un punto interior y en la superficie

Esquema del potencial eléctrico creado en una superficie

E_A =	1	·	Q
	4·π·ε₀		r²

V_A =	Q
	4·π·ε

Demo anterior con R = r

E_B = 0

V_B = V_A =	Q
	4·π·ε

Superficies equipotenciales

Gráfico del campo eléctrico en función de la distancia

Gráfico del potencial eléctrico en función de la distancia

• Ver ejemplo nº 1 - AP07

• Ver ejemplo nº 2 - AP07

• Ver ejemplo nº 3 - AP07

• Fuente:

Física de 2° de Bachillerato - Colegio Montpellier

Autor: Leandro Bautista. España.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet).

‹ Anterior
|
Siguiente ›

Ejemplos de aplicación