Sistema de nodos. Circuitos eléctricos
Sistema de nodos
Metodología para resolver circuitos de corriente eléctrica por el sistema de nodos.
a) Esquema de un circuito con fuente y resistencia:
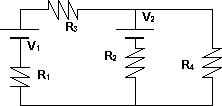
Ejemplo de circuito con fuente y resistencia
b) Esquema del circuito para resolver por el método de nodos
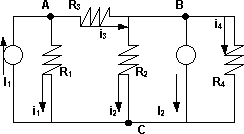
Circuito equivalente para resolver por el método de nodos
c) Transformar las fuentes de tensión en fuentes de corriente como:
| I1 = | V1 |
| R1 |
e
| I2 = | V2 |
| R2 |
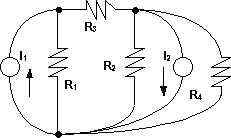
Circuito transformado con fuentes de corriente
d) Plantear el número de ecuaciones igual al número de nodos menos uno, que se tendrá de referencia.
Hay 3 nodos ⟶ 2 ecuaciones.
Nodo C: tomado como referencia.
Nodo A: I1 - i1 - i3 = 0
Nodo B: i3 - i2 - I2 - i4 = 0
Luego:
Nodo A: I1 = i1 + i3
Nodo B: - I2 = i2 + i4 - i3
Pero G es la conductancia (inversa de la resistencia):
| i1 = | VA |
| R1 |
i1 = VA·G1
i3 = (VA - VB)·G3
i2 = VB·G2
i4 = VB·G4
Reemplazando en "a" y "b":
Nodo A:
I1 = VA·G1 + (VA - VB)·G3
I1 = VA·G1 + VA·G3 - VB·G3
I1 = VA·(G1 + G3) - VB·G3
Nodo B:
-I2 = VB·G2 + VB·G4 - (VA - VB)·G3
-I2 = VB·G2 + VB·G4 - VA·G3 + VB·G3
-I2 = -VA·G3 + VB·(G2 + G4 + G3)
Ejemplos de aplicación
• Ver ejemplo n° 3 - para resolver
Autor: Ricardo Santiago Netto. Argentina
¿Qué es un nodo y una malla?