Teorema de Norton: Circuitos eléctricos

Es el recíproco del Teorema de Thevenin y dice: "Todo circuito compuesto de generadores y resistencias se puede reemplazar por un generador de corriente I_N en paralelo con una resistencia R_N ".

Dónde I_N es igual a la corriente que circula por los terminales de salida cuando estas se ponen en cortocircuito. R_N es la misma que la de Thevenin.

Para determinar el equivalente de Norton del circuito, se procede de la siguiente forma:

1) Cortocircuitamos C y D y calculamos la corriente que circula:

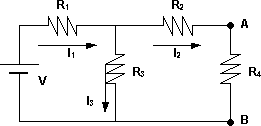
Esquema de un circuito con fuente y resistencia

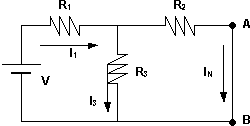
Selección del circuito para reemplazar por un corto-circuito

//: significa que están en paralelo

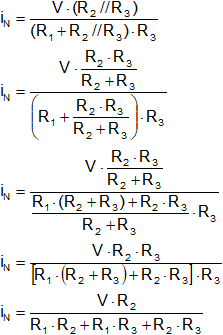
2) La R_N se calcula como en Thevenin:

R_N = R_TH

R_N = (R₁ // R₃) + R₂

3) Luego reemplazamos por el circuito equivalente:

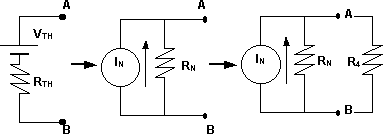
Esquema del reemplazo por el circuito equivalente

Ejemplos de aplicación

• Ver ejemplo n° 1 - resuelto

• Ver ejemplo n° 2 - resuelto

Autor: Ricardo Santiago Netto. Argentina

¿Qué indica el teorema de Norton?