Problema nº 2 de principio de Arquímedes. Estática de los fluidos - TP02

Enunciado del ejercicio nº 2

Un cuerpo tiene un volumen de 45 dm³, si su peso específico es de 2,7 gf/cm³, ¿cuál es el empuje que recibe sumergido en agua y su peso aparente?

ρ = 2,7 gf/cm³

V_cuerpo = V_d = 45 dm³

δ_agua = 1.000 kg/m³

Principio de Arquímedes:

E = δ·g·V_d (Empuje) (1)

Pa = P - E (Peso aparente) (2)

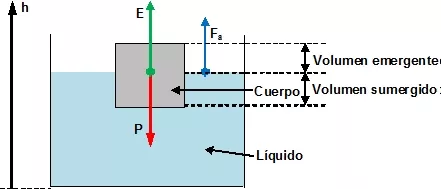
Principio de Arquímedes

En éste caso nos dan como dato el peso específico (ρ) en lugar de la densidad (δ), por lo tanto, es sencillo hallar el peso del cuerpo:

P = ρ·V

Convertimos las unidades:

ρ = 2,7 gf/cm³ = 26.477,955 N/m³

V_d = 45 dm³ = 0,0045 m³

Calculamos el peso:

P = (26.477,955 N/m³)·0,0045 m³

P = 1.191,508 N

Para responder la primer parte de la pregunta utilizamos la ecuación (1):

E = δ_agua·g·V_d

Adoptamos g = 10 m/s²

Calculamos el empuje:

E = (1.000 kg/m³)·(10 m/s²)·(0,0045 m³)

Resultado, el empuje es:

E = 450 N

Para la segunda parte de la pregunta utilizamos la ecuación (2):

Pa = P - E

Resolvemos:

Pa = 1.191,508 N - 450 N

Resultado, el peso aparente es:

Pa = 741,508 N

Si bien el peso aparente del cuerpo es menor que su peso real es evidente que el cuerpo se hunde porque E < Pa.

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, principio de Arquímedes