Problema nº 5 de principio de Arquímedes. Estática de los fluidos - TP02

Enunciado del ejercicio nº 5

Si el cubo del problema anterior se coloca en mercurio (δ = 13,6 g/cm³), ¿flota o se hunde?

δ_aluminio = 2,7 g/cm³

δ_mercurio = 13,6 g/cm³

l = 4 cm

Principio de Arquímedes:

E = δ·g·V_d (Empuje) (1)

Pa = P - E (Peso aparente) (2)

δ =	m
	V

V = l³ (Volumen del cubo)

Esquema de flotación
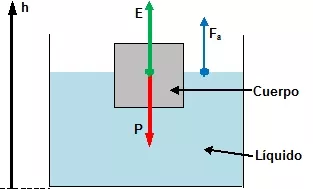
Principio de Arquímedes

Adecuamos las unidades:

δ_aluminio = 2,7 g/cm³ = 2.700 kg/m³

δ_mercurio = 13,6 g/cm³ = 13.600 kg/m³

l = 4 cm = 0,04 m

Para hallar la masa (m) usaremos la fórmula de densidad:

δ =	m
	V

Pero, primero, debemos calcular el volumen del cubo:

V = l³

V = (0,04 m)³

V = 0,000064 m³

Hallamos la masa del cubo de aluminio:

δ =	m
	V

m = δ·V

m = δ_aluminio·V

m = 2.700 kg/m³·0,000064 m³

m = 0,1728 kg

Ahora podemos aplicar la fórmula del Principio de Arquímedes:

Fa = δ·g·V_d - m·g

Cuando desconocemos el volumen de fluido desplazado por el cuerpo (V_d) empleamos el volumen del cuerpo.

V_d = 0,000064 m³

Adoptamos g = 10 m/s²

Reemplazamos en la fórmula de empuje:

Fa = (13.600 kg/m³)·(10 m/s²)·(0,000064 m³) - (0,1728 kg)·(10 m/s²)

Fa = 8,704 N - 1,728 N

Fa = 6,976 N

Resultado, como E > P ⇒ Fa > 0, entonces el cuerpo flota en el mercurio.

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, principio de Arquímedes