Problema nº 8 de principio de Arquímedes. Estática de los fluidos - TP02

Enunciado del ejercicio nº 8

¿Cuál será el volumen sumergido de un trozo de madera (δ = 0,38 g/cm³) de 95 dm³ al ser colocado en agua?

Desarrollo

Datos:

δ_madera = 0,38 g/cm³

δ_agua = 1.000 kg/m³

V_madera = 95 dm³

Fórmulas:

Principio de Arquímedes:

E = δ·g·V_d (Empuje) (1)

Pa = P - E (Peso aparente) (2)

Esquema:

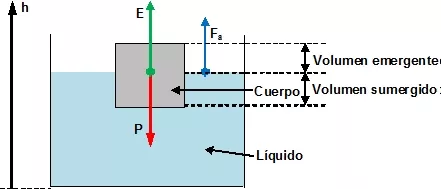
Principio de Arquímedes

Solución

Por tratarse de un cuerpo que está flotando en equilibrio (estático) la fuerza ascensional (Fa) es nula. Entonces:

Fa = δ_agua·g·V_d - m_madera·g = 0

δ_agua·g·V_d - m_madera·g = 0

δ_agua·g·V_d = m_madera·g

Cancelamos la aceleración de la gravedad:

δ_agua·V_d = m_madera

Y despejamos el volumen desplazado:

Para aplicar ésta fórmula primero debemos hallar la masa del trozo de madera utilizando la fórmula de densidad:

m_madera = δ_madera·V

Adecuamos las unidades:

δ_madera = 0,38 g/cm³ = 380 kg/m³

V_madera = 95 dm³ = 0,095 m³

Calculamos:

m_madera = δ_madera·V

m_madera = 380 kg/m³·0,095 m³

m_madera = 36,1 kg

Reemplazamos la masa del trozo de madera en la ecuación (1):

Y resolvemos:

Resultado, el volumen sumergido es:

V_d = 0,0361 m³

⚠ Ver apunte de "Principio de Arquímedes".

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP02
• | Siguiente ›

Ejemplo, principio de Arquímedes