Problema nº 9 de principio de Pascal. Estática de los fluidos - TP02

Enunciado del ejercicio nº 9

El radio del émbolo menor de una prensa es de 4 cm, si sobre él se aplica una fuerza de 60 N se obtiene en el otro émbolo una de 300 N, ¿cuál es el radio de éste émbolo?

Desarrollo

Datos:

r₁ = 4 cm

F₁ = 60 N

F₂ = 300 N

Fórmulas:

A = π·r² (Área del círculo)

Esquema:

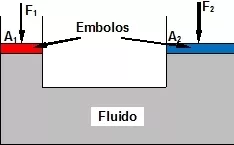
Principio de Pascal

Solución

Dónde la presión p es constante.

Despejamos el área A₂:

Convertimos las unidades de longitud:

r₁ = 4 cm = 0,04 m

Calculamos el área del émbolo con la fórmula de superficie del círculo:

A₁ = π·r₁²

A₁ = 3,14·(0,04 m)²

A₁ = 0,00503 m²

Calculamos el área A₂:

A₂ = 0,025 m²

Ahora debemos hallar el radio, por lo tanto, de la fórmula de área del círculo despejamos el radio:

A₂ = π·r₂²

Calculamos:

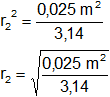
Resultado, el radio del émbolo es:

r₂ = 0,09 m

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP02
• | Siguiente ›

Ejemplo, principio de Pascal