Problema n° 10 de principio de Pascal. Estática de los fluidos - TP02
Enunciado del ejercicio n° 10
Sobre el émbolo menor de una prensa se aplica una fuerza de 50 N, si en el otro se obtiene una de 1.000 N, ¿cuál es la relación entre los radios de los émbolos?
Desarrollo
Datos:
F1 = 50 N
F2 = 1.000 N
Fórmulas:
| p = | F1 | = | F2 |
| A1 | A2 |
Esquema:
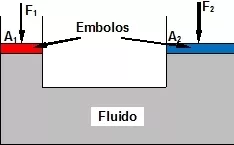
Esquema de una prensa hidráulica: principio de Pascal
Solución
Dónde la presión p es constante.
| F1 | = | F2 |
| A1 | A2 |
Para hallar la relación entre los radios debemos presentar la fórmula de la siguiente forma:
| F1 | = | A1 |
| F2 | A2 |
Desarrollamos las fórmulas de las áreas de los émbolos:
| F1 | = | π·r1² |
| F2 | π·r2² |
Cancelamos π en el segundo término:
| F1 | = | r1² |
| F2 | r2² |
Y resolvemos:
| r1² | = | 50 N |
| r2² | 1.000 N |
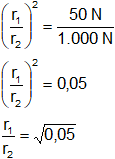
Resultado, la relación entre los radios de los émbolos es:
| r1² | = | 1 |
| r2² | 20 |
El resultado no tiene unidades por tratarse de una relación, por la misma razón se presenta como una fracción.
- ‹ Anterior
- |
- Regresar a la guía TP02
- |
- Siguiente ›
Autor: Ricardo Santiago Netto (Administrador de Fisicanet)
San Martín. Buenos Aires. Argentina.
Ver condiciones para uso de los contenidos de fisicanet.com.ar