Problema nº 11 de principio de Pascal. Estática de los fluidos - TP06

Enunciado del ejercicio nº 11

¿Qué fuerza ejercerá el pistón menor de un sillón de dentista para elevar a un paciente de 85 kg? Si el sillón es de 300 kg y los émbolos son de 8 cm y 40 cm de radio.

Desarrollo

Datos:

m_paciente = 85 kg

m_sillón = 300 kg

r₁ = 8 cm

r₂ = 40 cm

g = 9,81 m/s²

Fórmulas:

A = π·r² (Área del círculo)

Esquema:

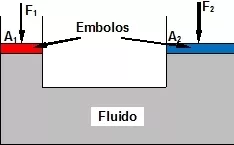
Principio de Pascal

Solución

Dónde la presión p es constante.

La fuerza que se ejerce sobre el pistón mayor es la fuerza peso. Por lo tanto primero debemos hallar el peso que debe levantar el pistón mayor, para ello recurrimos a la fórmula de peso:

P = m·g

La masa total que hay que levantar es:

m_T = m_paciente + m_sillón

m_T = 85 kg + 300 kg

m_T = 385 kg

Ahora podemos calcular el valor de la fuerza peso:

P = m_T·g

P = 385 kg·9,81 m/s²

P = 3.776,85 kg·m/s² = 3.776,85 N

Por lo dicho anteriormente:

F₂ = P = 3.776,85 N

Para aplicar el Principio de Pascal debemos despejar la fuerza F₁:

Y calcular el área de cada pistón con la fórmula de superficie del círculo:

Adecuamos las unidades:

r₁ = 8 cm = 0,08 m

r₂ = 40 cm = 0,4 m

Calculamos áreas:

A₁ = π·r₁²

A₁ = 3,14·(0,08 m)²

A₁ = 0,020106 m²

A₂ = π·r₂²

A₂ = 3,14·(0,4 m)²

A₂ = 0,502655 m²

Finalmente calculamos la fuerza F₁:

Resultado, la fuerza que ejercerá el pistón es:

F₁ = 151,074 N

⚠ Ver apunte de "Prensa hidráulica".

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP06
• | Siguiente ›

Ejemplo, principio de Pascal