Problema nº 1 de polea fija - TP02

Enunciado del ejercicio nº 1

Dos pesos de 10 N están suspendidos en los extremos de una cuerda que pasa por una polea ligera sin rozamiento. La polea está sujeta a una cadena que cuelga del techo. Determinar:

a) La tensión de la cuerda.

b) La tensión de la cadena.

Desarrollo

Datos:

P₁ = P₂ = 10 N

Fórmulas:

P = m·g

∑F = 0 (condición de equilibrio)

Condición de equilibrio: La sumatoria de los momentos de las fuerzas debe ser nula: Primera ley de Newton (equilibrio)

Solución

Primero realizamos un esquema para visualizar correctamente el enunciado:

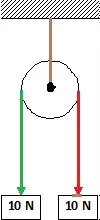
a)

Realizamos el diagrama del cuerpo libre para una de las cuerdas:

Planteamos las condiciones de equilibrio:

∑F = 0

P₁ - T₁ = 0

Despejamos T₁:

T₁ = P₁

Reemplazamos por el valor de P:

T₁ = 10 N

El mismo resultado se obtendrá para T₂:

Resultado, tensión de la cuerda es:

T₁ = T₂ = 10 N

b)

Realizamos el diagrama del cuerpo libre para la cadena:

Planteamos las condiciones de equilibrio:

∑F = 0

P - T = 0

En éste caso el peso P es la suma de los pesos que cuelgan de las cuerdas:

P = P₁ + P₂

P = 10 N + 10 N

P = 20 N

Despejamos la tensión T:

T = P

Resultado, tensión de la cadena es:

T = 20 N

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP02
• | Siguiente ›

Ejemplo, cómo calcular fuerzas, potencia, resistencia y pesos en poleas y aparejos. Problemas de estática resueltos y fáciles.