Problema nº 2 de palanca de primer género - TP03

Enunciado del ejercicio nº 2

¿Cuál es la potencia que equilibra una palanca cilíndrica, pesada, homogénea de 3 m de longitud y 25 kgf de peso, si esta apoyada en un punto que dista 90 cm del extremo donde se ha aplicado una resistencia de 350 kgf?

Desarrollo

Datos:

F₁ = 25 kgf

F₂ = 350 kgf

d₁ = 0,6 m (desde el apoyo)

d₂ = 0,9 m

d₃ = 2,1 m

Fórmulas:

Condición de equilibrio ⟶ MF = 0

MF = ∑(F·d) = F₁·d₁ + F₂·d₂ + F₃·d₃

Esquema:

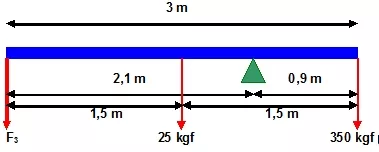
Solución

Si MF = 0, entonces:

0 = F₁·d₁ + F₂·d₂ + F₃·d₃

F₁·d₁ + F₂·d₂ = -F₃·d₃

F₂ es negativa porque gira en sentido horario.

Reemplazamos por los valores y calculamos:

Resultado, la potencia que equilibra una palanca es:

F₃ = 142,86 kgf

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP03
• | Siguiente ›

Ejemplo, cómo calcular fuerzas, potencia, resistencia y pesos en palancas. Problemas de estática resueltos y fáciles.