Problema nº 6 de palanca de primer género - TP03

Enunciado del ejercicio nº 6

Calcule cuál es la longitud de la barra, para que se mantenga en equilibrio, al aplicársele las fuerzas indicadas en la figura.

d_F = 5,00 m

d_P = ½·x - 5 m

d = x m

F = 30 kgf

P = 150 kgf

Condición de equilibrio: La sumatoria de los momentos de todas las fuerzas con respecto a un punto debe ser nulo:

∑M = 0

La suma de los momentos de las potencias debe ser igual a la suma de los momentos de las resistencias:

MP = MR

Desglosando las ecuaciones:

P·d_P = F·d_F

Condición de equilibrio: La sumatoria de los momentos de las fuerzas debe ser nula: Primera ley de Newton (equilibrio)

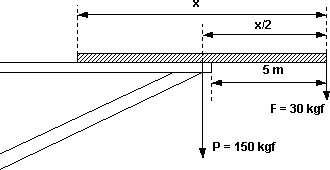
Palanca de primer género

P·(½·x - 5 m) = F·d_F

150 kgf·(½·x - 5 m) = 30 kgf·5 m

150 kgf·½·x - 150 kgf·5 m = 30 kgf·5 m

150 kgf·½·x - 750 kgm = 150 kgm

150 kgf·x = 2·(750 kgm + 150 kgm)

Resultado, la longitud de la barra para mantener el equilibrio es:

x = 12 m

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular fuerzas, potencia, resistencia y pesos en palancas. Problemas de estática resueltos y fáciles.