Problema nº 1 de condición de equilibrio. Cuerpos apoyados y coeficiente de rozamiento - TP05
Enunciado del ejercicio nº 1
Un bloque es arrastrado hacia la derecha a velocidad constante por una fuerza de 10 N que actúa formando un ángulo de 30° sobre la horizontal. El coeficiente de rozamiento entre el bloque y le superficie es de 0,50. ¿Cuál es el peso del bloque?
Desarrollo
Datos:
F = 10 N
α = 30°
μ = 0,50
Fórmulas:
Condición de equilibrio (Primera ley de Newton):
∑Fₓ = 0
∑Fy = 0
∑MF = 0
Fuerza de rozamiento (Rozamiento):
FR = μ·N
Esquema:
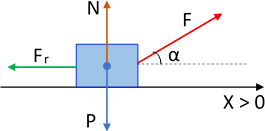
Esquema del cuerpo y las fuerzas
Solución
Primero realizamos los diagramas del cuerpo libre. Para esto elegimos la dirección y el sentido de los ejes convenientemente.
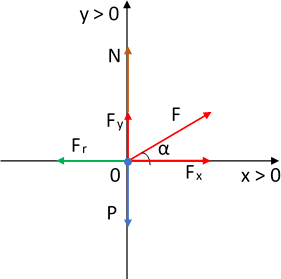
N = reacción normal al vínculo.
El sistema está en equilibrio, avanza con velocidad constante.
En el eje X las fuerzas son:
Fₓ - Fᵣ = 0
En el eje Y las fuerzas son:
N + Fy - P = 0
Siendo:
Fₓ = F·cos α
Fy = F·sen α
En el eje X reemplazamos Fₓ y Fᵣ:
Fₓ - Fᵣ = 0
F·cos α - μ·N = 0
Despejamos "N":
F·cos α = μ·N
![]()
En el eje Y reemplazamos N y Fy:
N + Fy - P = 0
![]()
Despejamos el peso "P":
![]()
Reemplazamos por los datos y calculamos:
![]()
P = 20 N·0,866 + 10 N·0,5
P = 17,32 N + 5 N
Resultado, el peso del bloque es:
P = 22,32 N
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP05
- | Siguiente ›
Ejemplo, cómo calcular el peso de un cuerpo. Problemas de estática resueltos y fáciles.