Problema nº 2 de condición de equilibrio. Cuerpos apoyados y suspendidos, coeficiente de rozamiento - TP05
Enunciado del ejercicio nº 2
El bloque a de la figura pesa 100 N, el coeficiente de rozamiento entre el bloque y la superficie es de 0,30. El bloque b pesa 20 N y el sistema está en equilibrio. Determinar:
a) El valor de la fuerza de rozamiento ejercida sobre el bloque A.
b) El peso máximo que puede tener el bloque B para que el sistema permanezca en equilibrio.
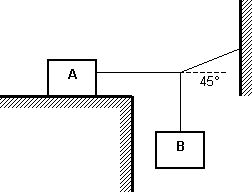
Desarrollo
Datos:
mA = 100 N
mB = 20 N
μ = 0,30
Fórmulas:
Condición de equilibrio (Primera ley de Newton):
∑Fₓ = 0
∑Fy = 0
∑MF = 0
Fuerza de rozamiento (Rozamiento):
FR = μ·N
Solución
Primero realizamos los diagramas de los cuerpos libres. Para esto elegimos la dirección y el sentido de los ejes convenientemente.
Simbología:
T = tensión en las cuerdas.
N = reacción normal al vínculo.
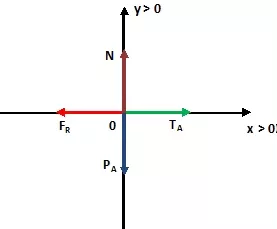
Cuerpo A:
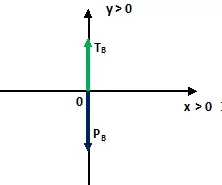
Cuerpo B:
Punto de sujeción fijo de la cuerda inclinada:
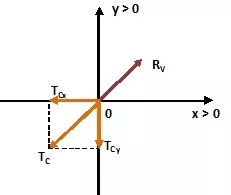
En el punto donde se unen las cuerdas tenemos es siguiente esquema:
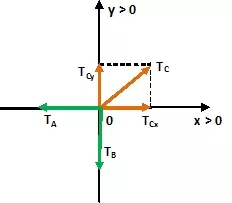
El sistema está en equilibrio, no hay movimiento, por lo tanto, se deben dar las siguientes condiciones para cada diagrama:
1) FR = TA;
2) TB = PB;
3) TC = RV (reacción del vínculo)
En éste punto el equilibrio será:
En el eje X las fuerzas son:
TA = TCx
En el eje Y las fuerzas son:
TCy = TB
Resolviendo:
a)
En el eje Y tenemos:
PB = 20 N;
TB = PB;
TB = TCy
Y,
TCy = TC·sen 45°;
Por lo tanto, reemplazando:
TB = 20 N
TCy = 20 N
TC·sen 45° = 20 N
![]()
TC = 28,28 N
Con este dato podemos hallar los valores de las fuerzas sobre el eje X, comenzando por:
TCx = TC·cos 45°
TCx = 28,28 N·cos 45°
TCx = 20 N
Luego tenemos:
FR = TA;
TA = TCx;
Por lo tanto:
FR = TCx
Resultado, la fuerza de rozamiento ejercida sobre el bloque A es:
FR = 20 N
b)
Para este punto debemos comenzar con la fuerza necesaria para vencer la fuerza de rozamiento del cuerpo A. Por definición:
FR = μ·N
FR = 0,30·100 N
FR = 30 N (fuerza de rozamiento a vencer = punto de equilibrio)
En el eje X:
TA = TCx, pero FR = TA, entonces:
FR = TCx = 30 N
Luego TCx es:
TCx = TC·cos 45°
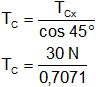
TC = 42,43 N (en equilibrio)
Hallamos el valor de la componente en Y:
TCy = TC·sen 45°
TCy = 42,43 N·sen 45°
TCy = 30 N
En el eje Y sabemos que:
TCy = TB, pero TCy = 30 N
Por lo tanto:
TB = 30 N (en equilibrio)
Continuando con los reemplazos en el eje Y:
PB = TB
Resultado, el peso del bloque B para que el sistema permanezca en equilibrio es:
PB = 30 N (peso necesario para romper el equilibrio)
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP05
- | Siguiente ›
Ejemplo, cómo calcular fuerzas en equilibrio y pesos suspendidos. Problemas de estática resueltos y fáciles.