Problema nº 10 de impulso y cantidad de movimiento, movimiento - TP03

Enunciado del ejercicio nº 10

Un hombre de 70 kg se encuentra sobre un trineo de 20 kg, en reposo sobre una superficie helada. El hombre tiene en sus manos una escopeta, con la cual desea acelerar el trineo para que éste adquiera una velocidad de 0,2 m/s.

Si en un disparo la escopeta ejerce un impulso de 25 kg·m/s sobre el proyectil, y la masa de éste es de 35 g, ¿en qué dirección debe apuntar? (Despreciar la masa de la escopeta frente a la del hombre).

Desarrollo

Datos:

mₕ = 70 kg

mₜ = 20 kg

mₚ = 35 g = 0,035 kg

v_f = 0,2 m/s

Iₑₚ = 25 kg·m/s

Fórmulas:

I = m·v

Solución

Primero calculamos el impulso que necesita el trineo aplicando la fórmula de impulso:

Iₕₜ = m_Total·v_f

Para esto debemos calcular la masa total a mover:

m_Total = mₕ + mₜ

m_Total = 70 kg + 20 kg

m_Total = 90 kg

El impulso que necesita el trineo será:

Iₕₜ = 90 kg·0,2 m/s

Iₕₜ = 18 kg·m/s

Dado que para acelerar el trineo solo se necesita un impulso de 18 kg·m/s sobre la horizontal y, el impulso de la escopeta es superior a lo necesario, el hombre deberá apuntar su escopeta formando un ángulo con la horizontal.

El impulso es una magnitud vectorial, por lo tanto, podemos resolver el problema utilizando trigonometría.

Siendo:

Iₕₜ = 18 kg·m/s: la componente horizontal.

Iₑₚ = 25 kg·m/s: la hipotenusa.

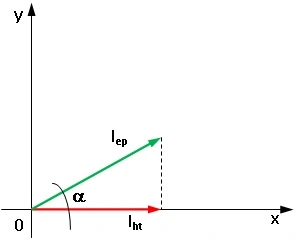
Diagrama de la descomposición del vector impulso

cos α =	Iₕₜ
	Iₑₚ

cos α =	18 k·m/s
	25 kg·m/s

cos α =	18
	25

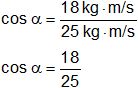
cos α = 0,72

Calculamos el ángulo:

α = arccos 0,72

α = 0,767 rad

Resultado, la dirección en que debe apuntar la escopeta es:

α = 43,95° (hacia arriba)

Enviado por Mauricio

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular el movimiento empleando el impulso