Ecuaciones del movimiento armónico simple (parte I)
Características de un movimiento armónico simple
- Vibración u oscilación: Distancia recorrida por la partícula en un movimiento completo de vaivén
- Centro de oscilación, O: punto medio de la distancia que separa las dos posiciones extremas alcanzadas por la partícula móvil
- Elongación, y. Distancia que en cada instante separa la partícula móvil del centro de oscilación O, tomado como origen de las elongaciones. Coordenada de la posición de la partícula en un momento dado. Consideramos positivos las valores de esta coordenada a la derecha del punto O y negativos a la izquierda
- Amplitud A, valor máximo de la elongación
- Período T, tiempo empleado por la partícula en efectuar una oscilación completa
- Frecuencia, f o n, número de oscilaciones efectuadas en la unidad de tiempo. Inversa del período f = 1/T (Hz)
- Pulsación o frecuencia angular o velocidad angular, ω, número de períodos comprendidos entre 2·π unidades de tiempo. ω = 2·π/T = 2·π·f·rad/s
Ecuación fundamental del movimiento armónico simple
En la figura se ha representado la posición x de un péndulo que oscila después de haber sido desplazado un pequeño ángulo en función del tiempo. Se han representado dos oscilaciones completas.

Representación de un péndulo que oscila
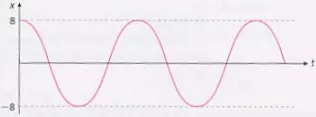
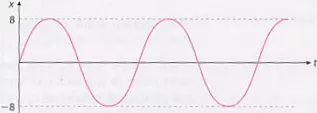
Si lo hacemos oscilar desde su posición vertical con un pequeño impulso obtendremos una gráfica similar solo que para t = 0, x = 0. La primera gráfica corresponde a un coseno y la segunda a un seno. Ambas gráficas representan el mismo movimiento con la única diferencia de la posición inicial de oscilación.
Si comparamos el movimiento del péndulo con el de una partícula que describe un movimiento circular, con radio igual a la de la amplitud de la oscilación y el mismo período (es decir, ajustamos la ω de la partícula para que coincida el T).
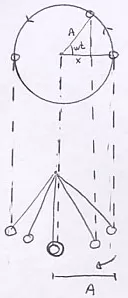
| Para un punto cualquiera de la trayectoria tenemos que su posición es: x = A·cos (ω·t). Puesto que A y ω son iguales para los dos movimientos y las posiciones respecto del origen van coincidiendo. La ecuación describe los dos movimientos. En general, si la elongación no es A, basta con introducir una fase que ajuste la posición inicial x = A·cos (ω·t + d). Para t = 0 ⇒ x = A·cos d |

|
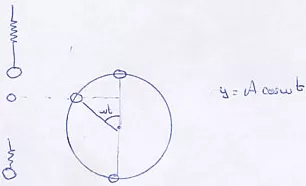
Si hablamos de un muelle ocurre exactamente lo mismo.
En general, la ecuación del movimiento armónico simple la escribiremos
| x = A·cos (ω·t + d) | ω·t + d: fase del movimiento. Al cabo de una oscilación completa la fase aumenta en 2·π rad y vuelve a la misma posición cos (ω·y + d) = cos (ω·t + d + 2·π) d: constante de fase o fase inicial. Si t = 0 se obtiene la posición inicial x₀ = A·cos d |
La ecuación puede escribirse indistintamente en función del seno o del coseno x = A·sen (ω·t + d)
A veces conviene usar una u otra:
1- Si hacemos oscilar un muelle o péndulo desde su máxima elongación, debe cumplirse que:
x₀ = A en t = 0 ⟶ Ecuación más sencilla es x = A·cos (ω·t) ya que cos 0 = 1. También se podría escribir:
x = A·sen (ω·t + π/2) ya que en t = 0 ⇒ x = A·sen π/2 = A.
Si la oscilación comienza en la posición de equilibrio se debe cumplir que:
x₀ = 0 en t = 0.
Lo más sencillo es x = A·sen (ω·t) pero también x = A·cos (ω·t ± π/2)
Si el movimiento se inicia en una posición intermedia, se puede elegir seno o coseno y calcular d a partir de x₀, A y ω.
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
- ‹ Anterior
- |
- Siguiente ›