Problema nº 1 de movimiento armónico simple, resortes - TP02

Enunciado del ejercicio nº 1

Un cuerpo de 4 kg de masa está sujeto aun resorte helicoidal, y oscila verticalmente con movimiento armónico simple. La amplitud es de 0,5 m, y en el punto más alto del movimiento el resorte tiene su longitud natural. Calcúlese la energía potencial elástica del resorte, la energía cinética del cuerpo, su energía gravitacional respecto al punto más bajo del movimiento y la suma de estas tres energías, cuando el cuerpo está:

a) En su punto más bajo.

b) En su posición de equilibrio, y cuando está en su punto de equilibrio la energía Eₚ = 0, porque X = 0.

c) En su punto más alto.

Desarrollo

Datos:

m = 4 kg

A = 0,5 m

Fórmulas:

k =	F
	x

Eₚ = ½·k·x²

Solución

k =	4 kg·9,8 m/s²
	0,5 m

k = 78,4 N/m

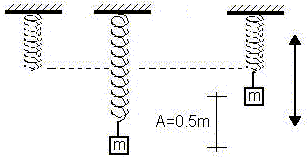
Esquema de los resortes sometidos a carga suspendida

Eₚ = ½·k·x²

E_c = ½·m·v² = 0

Eₚ = ½·78,4·5²

Eₚ = 9,8 J

E_c = 0 (porque su velocidad es cero).

E_pg = m·g·h/2 = 0 (porque la altura es 0).

E_T = Eₚ + E_c + E_pg = 9,8 N·m

V = √k/m·√A² - x²

V = 2,21 m/s

Entonces:

E_c = ½·4·2,21²

E_c = 9,76 J

E_pg = ½·m·g·h

E_pg = ½·4·9,8·0,5

E_pg = 9,8 J

E_T = Eₚ + E_c + E_pg = 19,56 J

Eₚ = ½·k·x²

E_c = ½·m·v² = 0

Como es en este caso para el punto más alto se considera la energía como negativa, definida así por su amplitud (-A).

Eₚ = ½·78,4·0,5²

Eₚ = -9,8 J

E_pg = ½·m·g·h

E_pg = 4·9,8·½

E_pg = 19,6 J

E_T = Eₚ + E_c + E_pg = 9,8 N·m

Autor: Jefferson Martínez Jara. Ecuador.

Ejemplo de cóamo resolver ejercicios de movimiento periódico con resortes