Problema nº 3 de movimiento armónico simple, resortes - TP02
Enunciado del ejercicio nº 3
Un bloque pequeño ejecuta un movimiento armónico simple en un plano horizontal con una amplitud de 10 cm. En un punto situado a 6 cm de distancia de la posición de equilibrio, la velocidad es de 24 cm/s.
a) ¿Cuál es el período?
b) ¿Cuál es el desplazamiento cuando la velocidad es ± 12 cm/s.
c) Si un pequeño cuerpo que oscila sobre el bloque se encuentra justo a punto de deslizar sobre el en el punto final de la trayectoria, ¿Cuál es el coeficiente de rozamiento?
Desarrollo
Datos:
A = 10 cm
x = 6 cm
v = 24 cm/s
v₂ = 12 cm/s
Fórmulas:
![]()
![]()
![]()
Esquema:
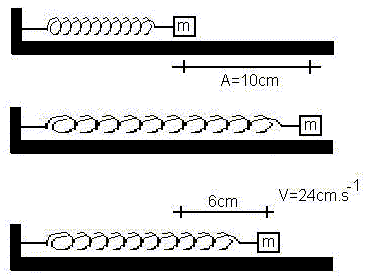
Esquema de resortes sometidos a elongación horizontal
Solución
a)
![]()
![]()
![]()
ω = 3 s⁻¹
![]()
Reemplazamos por los datos y calculamos:
![]()
T = 2,094 s
b)
![]()
![]()
Reemplazamos por los valores:
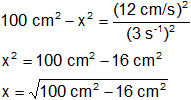
x = 9,16 cm
c)
a = ω²·x
a = 9·10 = 90 cm/s²
![]()
N = m·g
μ es el coeficiente de rozamiento, N es la normal. De aquí podemos sacar:
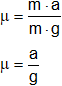
Reemplazamos por los valores y calculamos:
![]()
μ = 0,0918 (adimensional)
Nótese que las m (masa) en el instante de armar la ecuación se eliminan por lo que se extrae fácilmente el μ.
Autor: Jefferson Martínez Jara. Ecuador.
- ‹ Anterior |
- Regresar a la guía TP02
- | Siguiente ›
Ejemplo de cóamo resolver ejercicios de movimiento periódico con resortes