Problema nº 4 de movimiento armónico simple, resortes - TP02

Enunciado del ejercicio nº 4

Una fuerza de 30 N estira 15 cm un resorte vertical.

a) ¿Qué masa ha de suspenderse del resorte para que el sistema oscile con un período de (π/4) s.

b) Si la amplitud del movimiento es de 5 cm, ¿dónde está el cuerpo y en que dirección se mueve (π/12) s después de haber sobrepasado la posición de equilibrio, dirigiéndose hacia abajo?

c) ¿Qué fuerza ejerce el resorte sobre el cuerpo cuando está 3 cm por debajo de la posición de equilibrio y moviéndose hacia arriba?

Desarrollo

Datos:

F = 30 N

x = 15 cm = 0,15 m

A = 5 cm = 0,05 m

Fórmulas:

F = k·x

Esquema:

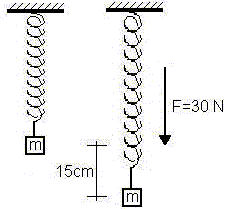
Esquema del resorte sometido a una carga suspendida

Solución

a)

m = ?

F = k·x

Reemplazamos por los datos y calculamos:

k = 200 N/m

Reemplazamos por los datos y calculamos:

m = 3,12 kg

b)

x = ?

x = 5·cos (8·t)

Se tiene que:

x = 4,33 cm

v = -40·sen 8·t

v = -20 cm/s; esto nos da a conocer que el cuerpo se está moviendo hacia el centro, desde abajo hacia arriba.

c)

Tenemos que cuando está 3 cm debajo de la posición de equilibrio la fuerza es:

F = -k·Δx

F = -6 N; pero como se necesita la fuerza total que es:

F_T = F_eq + F; entonces:

F_T = m·g + F

F_T = 3,125 kg·9,8 m/s² + 6 N

F_T = 36,6 N

Autor: Jefferson Martínez Jara. Ecuador.

• ‹ Anterior |
• Regresar a la guía TP02
• | Siguiente ›

Ejemplo de cóamo resolver ejercicios de movimiento periódico con resortes