Ejemplo de cóamo resolver ejercicios de movimiento periódico con resortes

Problema n° 5 de movimiento armónico simple - TP02

Enunciado del ejercicio n° 5

Un cuerpo de masa m se halla suspendido de un resorte helicoidal habiéndose medido el tiempo empleado en 100 oscilaciones completas para los siguientes valores de m:

m (g)
Tiempo empleado en 100 oscilaciones (s)

100
23,4

200
30,6

400
41,8

1.000
64,7

Dibújense las graficas de los valores medidos de:

a) T en función de m.

b) T² en función de m.

c) ¿Concuerdan los resultados experimentales con la teoría?

d) ¿Es alguna de las gráficas recta?

e) ¿Pasa la recta por el origen?

f) ¿Cuál es la constante de recuperación del resorte?

g) ¿Cuál es su masa?

Solución

a)

T = 2·π·√m/k

m	T
100 200 400 1.000	62,83 88,857 126,663 168,691

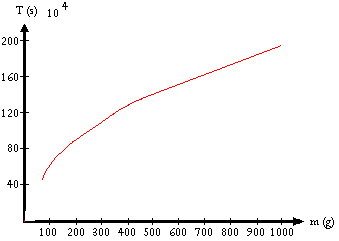
Gráfico del período en función de la masa

b)

T² = 4·π²·m/k

M	T²
100 200 400 1.000	0,39·10¨¨¨4/k 0,79·10¨¨4/¨k 1,5·10¨¨4/k 3,9·10¨¨4/k

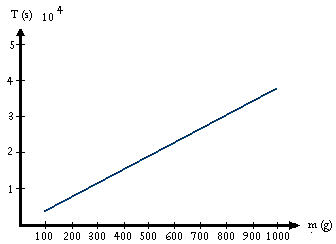
Gráfico del período en función de la masa

c)

Si, concuerdan por sus gráficas de t.

d)

Si la correspondiente a la de t²

e)

No pasan por el origen, si así fuera no existiría el movimiento, ya que la masa es cero.

f)

Haciendo algunas aproximaciones, utilizando la fórmula T² = 4·π²·m/k, se tiene que K = 8,52 din·cm

g)

La masa del resorte utilizando aproximaciones, m = k·(T/2·π)² = 18,17 g.

Autor: Jefferson Martínez Jara

Ecuador.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet)

Ver condiciones para uso de los contenidos de fisicanet.com.ar

🔍
✉ f t