Problema nº 5 de movimiento armónico simple, resortes - TP03
Enunciado del ejercicio nº 5
Dos resortes de la misma longitud natural pero con diferentes constantes de recuperación k1, y k2, se encuentran unidos a un bloque de masa m, situado sobre una superficie horizontal sin rozamiento. Calcúlese la constante de recuperación efectiva en cada uno de los tres casos (a), (b) y (c), representados en la figura.
a)
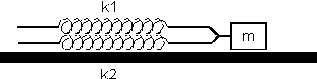
Esquema de resortes sometidos a elongación horizontal
b)
Esquema:

Esquema de resortes sometidos a elongación horizontal
c)
Esquema:
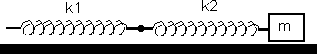
Esquema de resortes sometidos a elongación horizontal
Solución
a)
F = k·x
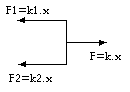
Esquema de las fuerzas
F = F₁ + F₂
k·x = k₁·x + k₂·x
k = k₁ + k₂
b)
F = k·x
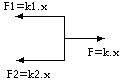
Esquema de las fuerzas
F = F₁ + F₂
k·x = k₁·x + k₂·x
k = k₁ + k₂
c)
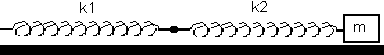
Esquema de resortes sometidos a elongación horizontal
x₁ = L₁ - L₀
x₂ = L₂ - L₀
x = x₁ + x₂
F = k·x
![]()
![]()
Por lo que es la misma fuerza:

Resortes en paralelo también conocido.
Autor: Jefferson Martínez Jara. Ecuador.
- ‹ Anterior |
- Regresar a la guía TP03
- | Siguiente ›
Ejemplo de cóamo resolver ejercicios de movimiento periódico con resortes