Guía nº 3 de ejercicios resueltos de movimiento armónico
Resolver los siguientes ejercicios
� Ver resolución de los ejercicios al pie de la página
Problema nº 1
Cuatro pasajeros con una masa total de 300 kg observan que al entrar en un automóvil los amortiguadores se comprimen 5 cm. Si la carga total que soportan los amortiguadores es de 900 kg, hállese el período de oscilación del automóvil cargado.
• Respuesta: T = 0,777 s
Problema nº 2
a) Un bloque suspendido de un resorte oscila con movimiento armónico simple. En el instante en que el desplazamiento es igual a la mitad de la amplitud, ¿Qué fracción de la energía total del sistema es cinética y cuál potencial? Supóngase l = 0 en la posición de equilibrio.
b) Cuándo el bloque está en equilibrio, la longitud del resorte es mayor en una cantidad que cuando no está estirado. Demuéstrese que ![]()
• Respuesta:
a) ![]()
b) ![]()
Problema nº 3
a) ¿Con qué fuerza ha de tirarse de un resorte vertical que mantiene en equilibrio cuerpo de 4 kg, para que al soltarlo realice 48 oscilaciones completes en 32 s con una amplitud de 5 cm?
b) ¿Qué fuerza ejerce el resorte sobre el cuerpo cuando se encuentra en el punto más bajo, en el centro y en el punto más alto de su trayectoria?
c) ¿Cuál es la energía del sistema cuando el sistema se encuentra 2 cm por debajo del punto medio de la trayectoria ¿¿Cuál es su energía potencial? (supóngase U = 0 en la posición de equilibrio.)
• Respuesta:
a) F = 17,8 N;
b) Fresorte = 21,47 N;
c) ET = 0,071 J, Ec = 0,373 J
Problema nº 4
Una fuerza de 60N estira 30 cm cierto resorte. Se cuelga del resorte un cuerpo de 4 kg de masa y se le deja llegar al reposo. Después se tira hacia abajo 10 cm y se abandona a sí mismo.
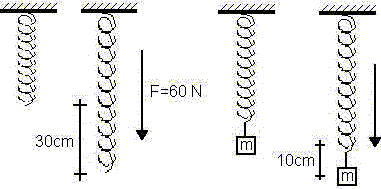
a) ¿Cuál es el período del movimiento?
b) ¿Cuáles son la magnitud y dirección de la aceleración del cuerpo cuando se encuentre 5 cm por encima de la posición de equilibrio, moviéndose hacia arriba?
c) ¿Cuál es la tensión del resorte cuando el cuerpo se encuentra 5 cm por encima de la posición de equilibrio?
d) Cuál es el tiempo mínimo necesario para pasar de la posición de equilibrio a la del punto situado 5 cm por encima?
e) Si se colocara un pequeño objeto sobre el cuerpo que oscila, ¿permanecería en contacto con el cuerpo, o no?
f) Si se colocara un pequeño objeto sobre el cuerpo que oscila y se duplica su amplitud, ¿dónde empezaría a separarse los dos cuerpos?
• Respuesta:
a) T = 0,888 s;
b) a = 2,5 m/s²;
c) T = 10 N;
d) t = 0,12 s;
e) No
Problema nº 5
Dos resortes de la misma longitud natural pero con diferentes constantes de recuperación k1, y k2, se encuentran unidos a un bloque de masa m, situado sobre una superficie horizontal sin rozamiento. Calcúlese la constante de recuperación efectiva en cada uno de los tres casos (a), (b) y (c), representados en la figura.
a)
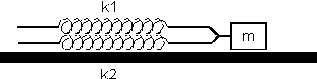
b)

c)
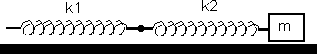
• Respuesta:
a) k = k₁ + k₂;
b) k = k₁ + k₂;
![]()
Problema nº 6
Un cuerpo de masa m suspendido de un resorte con constante de recuperación k, oscila con frecuencia f₁. Si el resorte se corta por el punto medio y se suspende el mismo cuerpo de una de las 2 mitades. La frecuencia es f₂. ¿Cuál es la relación de f₂/f₁?
• Respuesta: k₂ = 2·k₁
Problema nº 7
Dos resortes, de 0,2 m de longitud natural cada uno, pero con constantes de recuperación k1 y k2 diferentes, están unidos a las caras opuestas de un bloque de masa m situado sobre una superficie horizontal sin rozamiento. Los dos extremos de los resortes se fijan a dos clavos P1 y P2 situados a 10 cm de las posiciones iniciales de los resortes. Sean
k₁ = 1 N·m⁻¹
k₂ = 3 N·m⁻¹
m = 0,1 kg.
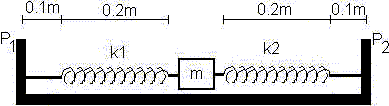
a) Calcúlese la longitud de cada resorte cuando el bloque está en la nueva posición de equilibrio, después de sujetar los resortes a los clavos.
b) Determínese el período de oscilación del bloque si este se desplaza ligeramente de su nueva posición de equilibrio y se abandona a si mismo.
• Respuesta:
a) L₁ = 0,1 m y L₂ es 0,3 m;
b) T = 0,993 s
Autor: Jefferson Martínez Jara. Ecuador.