Problema nº 4 de movimiento armónico simple, péndulo simple - TP04

Enunciado del ejercicio nº 4

¿Cuál es la variación Δt del período de un péndulo simple cuando la aceleración de la gravedad g varía en Δg?

Indicación: El nuevo período t + Δt se obtiene sustituyendo g por g + Δg:

Para obtener una expresión aproximada, desarróllese el factor (g + Δg)⁻^½ utilizando el teorema del binomio y considerando sólo los dos primeros términos:

(g + Δg)⁻^½ = g⁻^½ - ½·g⁻^3/2·Δg + …

Los otros términos contienen potencias más altas de Δg y son muy pequeños cuando Δg es pequeño.

Solución

Δt = ?

(g + Δg)⁻^½ = g^½ - ½·g⁻^3/2·Δg + …

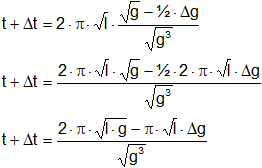
Resultado, la variación Δt del período del péndulo simple es:

Autor: Jefferson Martínez Jara. Ecuador.

• ‹ Anterior |
• Regresar a la guía TP04
• | Siguiente ›

Ejemplo de cóamo resolver ejercicios de movimiento periódico con péndulo simple