Guía nº 4 de ejercicios resueltos de movimiento armónico
Resolver los siguientes ejercicios
� Ver resolución de los ejercicios al pie de la página
Problema nº 1
El bloque representado en la figura, oscila con amplitud de 0,05 m. En el instante en que pasa por su posición de equilibrio, se deja caer verticalmente sobre el bloque una masa de barro de 0,1 kg que se adhiere a él.
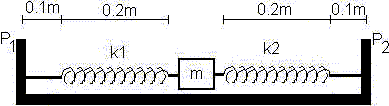
A = 0,05 m = 5 cm
m₁ = 0,1 kg
m₂ = 0,1 kg
k₁ = 1 N·m⁻¹
k₂ = 3 N·m⁻¹
a) Determínese el nuevo período.
b) ¿Ha habido pérdida de energía mecánica? En caso afirmativo, ¿en qué se emplea?
c) ¿Serían iguales las respuestas si se hubiera dejado caer la masa de barro sobre el bloque cuando este se encontrara en un extremo de su trayectoria?
• Respuesta:
a) T = 1,41 s;
b) Sí;
c) No
Problema nº 2
Un péndulo simple de 4 m de longitud oscila con amplitud de 0,2 m.
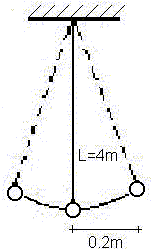
a) Calcúlese la velocidad del péndulo en el punto más bajo de la trayectoria.
b) Calcúlese la aceleración en los extremos de su trayectoria.
• Respuesta:
a) vₘ = 0,313 m/s;
b) aₘₐₓ = 0,49 m/s²
Problema nº 3
Determínese la longitud de un péndulo simple cuyo período es exactamente 1 s en un punto donde g = 9,80 m/s²
• Respuesta: l = 0,248 m
Problema nº 4
¿Cuál es la variación Δt del período de un péndulo simple cuando la aceleración de la gravedad g varía en Δg?
Indicación: El nuevo período t + Δt se obtiene sustituyendo g por g + Δg:
![]()
Para obtener una expresión aproximada, desarróllese el factor (g + Δg)⁻½ utilizando el teorema del binomio y considerando sólo los dos primeros términos:
(g + Δg)⁻½ = g⁻½ - ½·g⁻3/2·Δg + …
Los otros términos contienen potencias más altas de Δg y son muy pequeños cuando Δg es pequeño.
• Respuesta:

Problema nº 5
Un reloj de péndulo que funciona correctamente en un punto donde g = 9,80 m·s⁻² atrasa 10 s diarios a una altura mayor. Utilícense los resultados del ejercicio nº 4 para determinar el valor aproximado de g en la nueva localización.
• Respuesta: g = 10,00 m/s²
Problema nº 6
Cierto péndulo simple tiene en la tierra un período de 2 s ¿Cuál sería su período en la superficie de la luna, donde g = 1,7 m·s⁻²
• Respuesta: TLuna = 4,79 s
Problema nº 7
Se desea construir un péndulo de período 10 s.
a) ¿Cuál es la longitud de un péndulo simple que tenga este período?
b) Supóngase que el péndulo ha de montarse en una caja cuya altura no exceda de 0,5 m ¿Puede idearse un péndulo que satisfaga este requisito con un período de 10 s?
• Respuesta:
a) l = 24,8 m;
b) Sí
Autor: Jefferson Martínez Jara. Ecuador.