Problema nº 5 de movimiento armónico simple, péndulo simple - TP04

Enunciado del ejercicio nº 5

Un reloj de péndulo que funciona correctamente en un punto donde g = 9,80 m·s⁻² atrasa 10 s diarios a una altura mayor. Utilícense los resultados del ejercicio nº 4 para determinar el valor aproximado de g en la nueva localización.

Solución

Se determina en base a la ecuación desarrollada:

Despejando Δg nos queda:

Anteriormente se tiene que conocer l que va a ser un valor exagerado, pero solo es para valores de cálculo, por tanto:

Reemplazamos por los datos y calculamos:

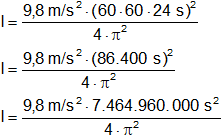
l = 5.821.617.892 m

Reemplazando en la ecuación anterior se determina el valor de la gravedad nueva.

Δg = 0,20 m/s²

Ahora el nuevo valor de la gravedad será: 10,00 m/s²

Autor: Jefferson Martínez Jara. Ecuador.

• ‹ Anterior |
• Regresar a la guía TP04
• | Siguiente ›

Ejemplo de cóamo resolver ejercicios de movimiento periódico con péndulo simple