Problema nº 5 de calorimetría, cantidad de calor y calorímetro de masas - TP03

Enunciado del ejercicio nº 5

En un calorímetro con 500 g de agua a 18 °C se introducen 150 g de cobre a 100 °C. Si la temperatura final es de 20,2 °C, ¿cuál es el calor específico del cobre?

Desarrollo

Datos:

m₁ = 500 g (agua) = 0,50 kg

tᵢ₁ = 18 °C

m₂ = 150 g (cobre) = 0,15 kg

tᵢ₂ = 100 °C

t_f = 20,2 °C

cₑ₁ = 1 kcal/kg·°C (agua)

Fórmulas:

Q = m·cₑ·(t_f - tᵢ) (1)

Solución

En el equilibrio térmico la temperatura final de la mezcla obviamente es única:

t_f1 = t_f2 = t_f

Para resolver el problema planteamos las ecuaciones de cantidad de calor (Q) para cada componente:

Q₁ = m₁·cₑ₁·(t_f1 - tᵢ₁) (3) para el agua.

Q₂ = m₂·cₑ₂·(t_f2 - tᵢ₂) (4) para el cobre

Debemos tener en cuenta que la temperatura final del cobre es menor que su temperatura inicial, por lo tanto:

Q₁ = m₁·cₑ₁·(t_f - tᵢ₁) (3) para el agua.

Q₂ = m₂·cₑ₂·(tᵢ₂ - t_f) (4) para el cobre

Planteamos el equilibrio:

Q₁ = Q₂

m₁·cₑ₁·(t_f - tᵢ₁) = m₂·cₑ₂·(tᵢ₂ - t_f)

Despejamos el calor específico del cobre (cₑ₂):

Reemplazamos por los datos:

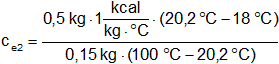
Hacemos las cuentas:

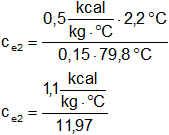
Resultado, el calor específico del cobre es:

cₑ₂ = 0,0912 kcal/kg·°C

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP03
• | Siguiente ›

Ejemplo, cálculos de cantidad de calor con calorímetro de masas