Guía nº 8 de ejercicios resueltos de plano inclinado y resortes
Resolver los siguientes ejercicios
� Ver resolución de los ejercicios al pie de la página
Problema nº 1
Un bloque de 5 kg de masa está sostenido por una cuerda que tira de él hacia arriba con una aceleración de 2 m/s²
a) ¿Cuál es la tensión de la cuerda?
b) Después de haberse puesto en movimiento el bloque, la tensión de la cuerda disminuye a 49 N. ¿Qué clase de movimiento tendrá entonces el bloque?
c) Si se afloja completamente la cuerda, se observa que el bloque asciende aún 2 m antes de detenerse. ¿Qué velocidad llevaba cuando se aflojó la cuerda?
• Respuesta:
a) T = 59 N;
b) MRU;
c) Vᵢ = 6,261 m/s
Problema nº 2
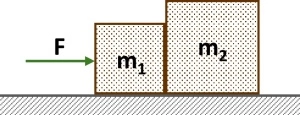
a) Calcular la aceleración que adquiere el sistema de la figura cuando se le aplica una fuerza F = 20 N, si m₁ = 4 kg y m₂ = 6 kg.
b) ¿Cuál es la fuerza que ejerce el bloque 1 sobre el bloque 2?
• Respuesta:
a) a = 2 m/s²;
b) F₁₂ = 12 N
Problema nº 3
Una caja de 15 kg de masa descansa sobre la plataforma de un camión. El coeficiente de rozamiento entre la caja y el suelo es de 0,1. El camión inicia su marcha con una aceleración de 1,5 m/s². Si la caja se encuentra a 4 m del final del camión cuando éste arranca, determinar:
a) ¿Cuánto tiempo transcurrirá hasta que la caja salga despedida del camión por su parte trasera?
b) ¿Qué distancia recorrerá el camión en ese tiempo?
• Respuesta:
a) 4 s;
b) 12 m
Problema nº 4
Un tren de pasajeros consta de una locomotora y dos vagones. La masa de la locomotora es de 6.000 kg y la de cada vagón es de 2.000 kg. El tren sale de una estación con una aceleración de 0,5 m/s², determinar:
a) La tensión en el enganche entre la locomotora y el primer vagón.
b) La tensión en el enganche entre los vagones.
c) La fuerza horizontal total que ejercen las ruedas de la locomotora sobre el riel.
• Respuesta:
a) 2.000 N;
b) 1.000 N;
c) 5.000 N
Problema nº 5
Un bloque descansa sobre un plano inclinado que forma un ángulo α con la horizontal. El coeficiente de rozamiento cinético es de 0,5 y el estático de 0,75. Calcular:
a) El valor de α para que el bloque comience a deslizarse.
b) La aceleración cuando el bloque comenzó a deslizarse.
c) El tiempo necesario para que el bloque se deslice 6,096 m por el plano inclinado.
• Respuesta:
a) 36,9°;
b) 1,95 m/s²;
c) 2,5 s
Problema nº 6
Un cuerpo de 10 kgf se desliza sobre un plano inclinado de 3 m de longitud y 0,6 m de altura. Suponiendo nulo el rozamiento, calcular su aceleración y el tiempo que tarda en recorrer el plano.
• Respuesta:
a) a = 1,96 m/s²;
b) t = 1,75 s
Problema nº 7
Calcular la aceleración del sistema de la figura, y la tensión de la cuerda.
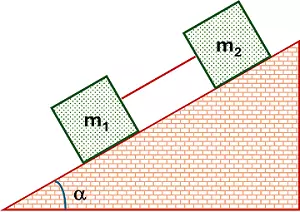
• Respuesta: a = g·sen α; T = 0
Problema nº 8
Se tiene el sistema de la figura, en donde m₁ = 40 kg y m₂ = 20 kg. Se sabe que el estiramiento que sufre el resorte y la tensión a la que está sometido son proporcionales: T = k·x; k = 30 N/m.
Calcular la fuerza F y el estiramiento del resorte cuando el sistema se acelera a razón de 4 m/s².

Figura 1
Problema nº 9
Si en el problema anterior (figura 1), el estiramiento del resorte es de 60 cm cuando el sistema se acelera, calcular su aceleración y la fuerza F.
• Respuesta: a = 0,9 m/s²; F = 54 N
Problema nº 10
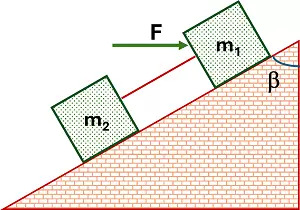
Se aplica una fuerza horizontal de 200 N sobre la masa m₁ = 4 kg de la figura (β = 60°).
Calcular el valor de m₂ y la tensión de la cuerda, si el sistema asciende con una aceleración de 0,1 m/s².
• Respuesta: m₂ = 30,64 kg; T = 153,2 N
Problema nº 11
Calcular la intensidad de la fuerza F que hace subir la masa m = 40 kg por el plano inclinado de ángulo α = 30° con una aceleración a = 2 m/s².
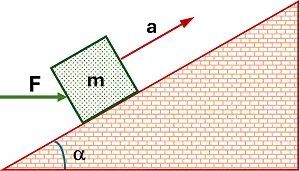
• Respuesta: F = 318,32 N
Bibliografía:
"Física". Hernán Miguel y Marcelo C. Cánepa. 1983. Argentina.
Autor: Ricardo Santiago Netto. Argentina