Problema nº 9 de estática de los fluidos - TP03

Enunciado del ejercicio nº 9

Un cuerpo pesa en el aire 18 N y en el agua 13 N, ¿cuál es su densidad?

Desarrollo

Datos:

P = 18 N (peso en aire)

Pa = 13 N (peso en agua)

g = 9,81 m/s²

δ_agua = 1.000 kg/m³

Fórmulas:

Principio de Arquímedes:

E = δ·g·V_d (Empuje) (1)

Pa = P - E (Peso aparente) (2)

Esquema:

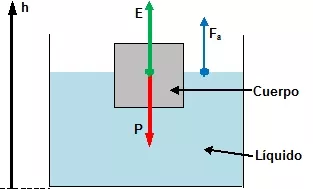
Principio de Arquímedes

Solución

El problema nos da el peso del cuerpo en el aire y el peso aparente en agua.

Sabemos que:

P = m·g

Con ésta ecuación hallaremos la masa del cuerpo:

Y que, según el principio de Arquímedes (2):

Pa = P - E

Por lo tanto:

E = P - Pa

Por lo que:

E = 18 N - 13 N

E = 5 N

Y, de (1):

E = δ_agua·g·Vd

Con ésta ecuación hallaremos el volumen del cuerpo:

Como el cuerpo se encuentra sumergido sabemos que el volumen desplazado (Vd) por el cuerpo es el volumen total del cuerpo.

Finalmente, con los resultados de las ecuaciones (4) y (5), calcularemos la densidad solicitada con la fórmula (3):

Calculamos la masa del cuerpo con la ecuación (4):

m = 1,8349 kg

Calculamos el volumen del cuerpo con la ecuación (5):

Sabemos que 1 N (newton) = 1 kg·m/s²

Vd = 0,00051 m³

Finalmente calculamos la densidad del cuerpo:

Resultado, la densidad del cuerpo es:

δ = 3.600 kg/m³ = 3,6 g/cm³

⚠ Ver apunte de "Principio de Arquímedes".

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP03
• | Siguiente ›

Ejemplo, principio de Arquímedes