Problema nº 2 de movimiento armónico simple, resortes - TP03

Enunciado del ejercicio nº 2

a) Un bloque suspendido de un resorte oscila con movimiento armónico simple. En el instante en que el desplazamiento es igual a la mitad de la amplitud, ¿Qué fracción de la energía total del sistema es cinética y cuál potencial? Supóngase l = 0 en la posición de equilibrio.

b) Cuándo el bloque está en equilibrio, la longitud del resorte es mayor en una cantidad que cuando no está estirado. Demuéstrese que

Solución

a)

x = ½·A

E_T = E_c + Eₚ

½·m·ω²·A² = E_c + ½·m·ω²·x²

E_c = ½·m·ω²·x² - ½·m·ω²·A²

Luego sustituímos A por 2·x, tenemos:

E_c = ½·m·ω²·x² - ½·m·ω²·4·x²

Despejamos para dejar en función de la energía total:

E_c = -½·3·m·ω²·x²

Luego volvemos a sustituír A en vez de x para que nos de la energía total, entonces armamos la ecuación:

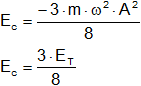
b)

P = m·g

F = P

X = s

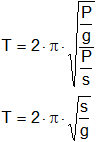
Autor: Jefferson Martínez Jara. Ecuador.

• ‹ Anterior |
• Regresar a la guía TP03
• | Siguiente ›

Ejemplo de cóamo resolver ejercicios de movimiento periódico con resortes