Problema nº 7 de movimiento armónico simple, resortes - TP03
Enunciado del ejercicio nº 7
Dos resortes, de 0,2 m de longitud natural cada uno, pero con constantes de recuperación k₁ y k₂ diferentes, están unidos a las caras opuestas de un bloque de masa m situado sobre una superficie horizontal sin rozamiento. Los dos extremos de los resortes se fijan a dos clavos P1 y P2 situados a 10 cm de las posiciones iniciales de los resortes. Sean
k₁ = 1 N/m
k₂ = 3 N/m
m = 0,1 kg.
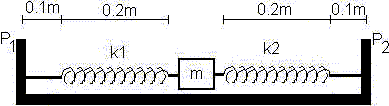
Esquema de resortes sometidos a elongación horizontal
a) Calcúlese la longitud de cada resorte cuando el bloque está en la nueva posición de equilibrio, después de sujetar los resortes a los clavos.
b) Determínese el período de oscilación del bloque si este se desplaza ligeramente de su nueva posición de equilibrio y se abandona a si mismo.
Solución
a)
Teniendo en cuenta que se tiene las longitudes originales a cuales las denominaremos Lo1 y Lo2 = 0,2 m, tendremos la resultante de las fuerzas por los 2 resortes:
x₁ = x₂ = 0,1 m
k₁ = 1 N/m
k₂ = 3 N/m
FT = F₁ + F₂
Deduciendo y aplicando F = k·x, tenemos:
Ktotal·xtotal = k₁·x₁ + k₂·x₂
Ktotal = k₁ + k₂; y,
xtotal = x₁ + x₂; por consiguiente:
4(x₁ + x₂) = k₁·x₁ + k₂·x₂
![]()
Desarrollando:
4·x₁ = k₁·(x₁ - x₂) + k₂·x₂
Dejamos todo para despejar x₂, que es el factor a sacar su valor:
![]()
Reemplazamos por los valores y calculamos:
![]()
x₂ = 0,3 m
xₜ = xₜ + x₂
x₁ = xₜ - x₂
x₁ = 0,2 - 0,3 = 0,1 m
Ahora L₁ = 0,1 m y L₂ es 0,3 m
b)
![]()
Reemplazamos por los datos y calculamos:
![]()
T = 0,993 s
Autor: Jefferson Martínez Jara. Ecuador.
- ‹ Anterior |
- Regresar a la guía TP03
- | Siguiente ›
Ejemplo de cóamo resolver ejercicios de movimiento periódico con resortes