Problema nº 2 de variación de la longitud ocasionada por la dilatación - TP02

Enunciado del ejercicio nº 2

Se tienen dos varillas de acero (α = 0,000012/°C). La primera tiene exactamente un metro de longitud a los 0 °C y la otra a los 30 °C. ¿Cuál será la diferencia de longitudes a los 18 °C?

Desarrollo

Datos:

t₁ₐ = 0 °C

t_1b = 30 °C

t₂ₐ = t_1b = 18 °C

l₁ₐ = 1 m

l_1b = 1 m

Fórmulas:

Δl = α·l₁·Δt°

Esquema:

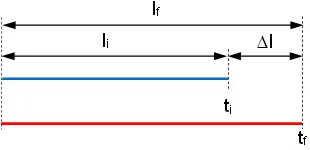
Solución

Utilizamos la ecuación de dilatación lineal para ambos casos y para conocer la longitud final, primero para la varilla que se encuentra a 0 °C a:

Δl = l₂ - l₁

l₂ₐ - l₁ₐ = α·l₁ₐ·Δt°ₐ

l₂ₐ = α·l₁ₐ·Δt°ₐ + l₁ₐ

l₂ₐ = (0,000012/°C)·1 m·(18 °C - 0 °C) + 1 m

l₂ₐ = (0,000012/°C)·m·18 °C + 1 m

l₂ₐ = 1,000216 m

Luego para la varilla que se encuentra a 30 °C:

l_2b - l_1b = α·l_1b·Δt°_b

l_2b = α·l_1b·Δt°_b + l_1b

l_2b = (0,000012/°C)·1 m·(18 °C - 30 °C) + 1 m

l_2b = (0,000012/°C)·m·(-12 °C) + 1 m

l_2b = -0,000144 m + 1 m

l_2b = 0,999856 m

Los resultados anteriores indican qué longitud tendrá cada una de las varillas a los 18 °C. Ahora calculamos la diferencia de longitud entre ambas:

Δl = l₂ₐ - l_2b

Δl = 1,000216 m - 0,999856 m

Resultado, la diferencia de longitud entre ambas a los 18 °C es:

Δl = 0,00036 m

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular la variación de longitud ocasionada por la dilatación. ¿Cómo calculo la dilatación lineal de una barra? ¿Cuánto aumenta el volumen del mercurio al calentarlo?