Problema nº 10 de trabajo y potencia, energía cinética y potencial en un plano inclinado - TP04

Enunciado del ejercicio nº 10

Un cuerpo de 2,45 kg de masa se desplaza sin rozamiento por un plano inclinado de 5 m y 1 m de altura, determinar:

a) La distancia recorrida por el cuerpo, que parte del reposo, en 1,5 s.

b) La energía cinética adquirida en ese lapso.

c) La disminución de la energía potencial en igual lapso.

Desarrollo

Datos:

m = 2,45 kg

d = 5 m

h = 1 m

t = 1,5 s

vᵢ = 0 m/s

Se adopta g = 10 m/s²

Fórmulas:

Δx = vᵢ·t + ½·a·t²

v_f² - vᵢ² = 2·a·Δx

E_c = ½·m·v²

Eₚ = m·g·h

Esquema:

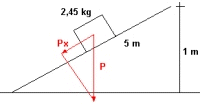
Esquema del cuerpo y la fuerza en un plano inclinado

Solución

a)

La componente Pₓ de la fuerza peso es la causante del desplazamiento.

Pₓ = P·sen α

Geométricamente:

Pₓ = P·0,2

De estas fuerzas obtenemos la aceleración del cuerpo en dirección del plano:

a·m = g·m·0,2

a = g·0,2

a = 10 m/s²·0,2

a = 2 m/s²

El espacio recorrido será:

e = ½·a·t²

e = ½·2 m/s²·(1,5 s)²

Resultado, la distancia recorrida por el cuerpo es:

e = 2,25 m

b)

Mediante cinemática calculamos la velocidad a los 1,5 s:

v_f² - vᵢ² = 2·a·e

v_f² - 0 = 2·2 m/s²·2,25 m

v_f = 3 m/s

E_c = ½·m·v_f²

E_c = ½·2,45 kg·(3 m/s)²

Resultado, la energía cinética adquirida en 1,5 s es:

E_c = 11,025 J

c)

Como la energía potencial depende de la altura calculamos que altura se corresponde con el desplazamiento de 2,25 m.

Por triángulos semejantes:

h = 0,45 m

Eₚ = m·g·h

Eₚ = 2,45 kg·10 m/s²·0,45 m

Resultado, la pérdida de energía potencial en 1,5 s es:

Eₚ = 11,025 J

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP04
• | Siguiente ›

Ejemplo, cómo calcular la energía cinética y potencial en un plano inclinado