Problema nº 6 de electrólisis. Primera ley de Faraday, masa depositada en un electrodo - TP06
Enunciado del ejercicio nº 6
Se utiliza una corriente de 15 A para niquelar con un baño de NiSO₄. En el cátodo se forman níquel e hidrógeno gaseoso. El rendimiento de la corriente en relación con la formación de níquel es el 60 %. Calcular:
a) ¿Cuántos gramos de níquel se depositan en el cátodo por hora?
b) ¿Cuál será el espesor del depósito si el cátodo está formado por una hoja de metal cuadrado de 4,0 cm de lado, teniendo en cuenta que el recubrimiento es por ambos lados? La densidad del níquel es de 8,908 g/cm³.
c) ¿Cuál será el volumen de hidrógeno que se forma por hora en CNPT?
Desarrollo
Datos:
i = 15 A
t = 1 h
η = 0,60
l = 4,0 cm
δNi = 8,908 g/cm³
ζNi = 0,000304 g/C (Dato de tabla)
EqH⁺ = 1,00797 g
EqNi²⁺ = 29,355 g
Fórmulas:
m = ζ·i·t
| m₁ | = | Eq₁ |
| m₂ | Eq₂ |
Solución
a)
Aplicamos la primera ley de Faraday:
m = ζ·i·t
Adecuamos las unidades:
t = 1 h = 1 h·(3.600 s/1 h)
t = 3.600 s
Reemplazamos y calculamos la masa teórica:
mT = 0,000304 g/C·15 A·3.600 s
m = 16,416 g
Calculamos la masa real según el rendimiento (η) indicado:
mR = η·mT
mR = 0,60·16,416 g
mR = 9,8496 g
Respuesta a): la masa de níquel que se deposita en el cátodo por hora es 9,85 g.
b)
Para calcular el espesor del recubrimiento primero debemos hallar la superficie total de la lámina de metal.
S = 2·l²
S = 2·(4,0 cm)²
S = 32 cm²
Luego debemos calcular que ocupa la masa depositada de níquel, empleamos la fórmula de densidad:
| δ = | m |
| V |
Despejamos V:
| V = | m |
| δ |
Reemplazamos y calculamos:
| V = | 9,8496 g |
| 8,908 g/cm³ |
V = 1,105702739 cm³
Dividiendo el volumen por la superficie obtenemos el espesor d:
| d = | V |
| S |
| d = | 1,105702739 cm³ |
| 32 cm² |
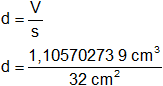
d = 0,034553211 cm
Respuesta b): el espesor de la capa de níquel que se deposita es 0,035 cm.
c)
Aplicamos la segunda ley de Faraday comparando con el níquel depositado (suponemos el mismo rendimiento).
| m₁ | = | Eq₁ |
| m₂ | Eq₂ |
| mH⁺ | = | EqH⁺ |
| mNi²⁺ | EqNi²⁺ |
Despejamos mH⁺:
| mH⁺ = | mNi²⁺·EqH⁺ |
| EqNi²⁺ |
Reemplazamos y calculamos:
| mH⁺ = | 9,8496 g·1,00797 g |
| 29,355 g |
mH⁺ = m₂ = 0,338208186 g
Con la masa del hidrógeno desprendido y, recordando que, 22,4 dm³ de cualquier gas en CNPT es el volumen molar:
| 2·1,00797 g | ⟶ | 22,4 dm³ |
| 0,338208186 g | ⟶ | V |
| V = | 0,338208186 g·22,4 dm³ |
| 2,01594 g |
| V = | 7,575863376 dm³ |
| 2,01594 |
V = 3,757980583 dm³
Respuesta c): el volumen de hidrógeno que se forma por hora en CNPT es 3,758 dm³.
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP06
- | Siguiente ›
Ejemplo, cómo calcular la masa de un elemento que se deposita en el electrodo