Determinación de la energía del electrón en el modelo de Bohr
La determinación de los niveles de energía Eₙ del electrón en el modelo de Bohr se efectúa combinando un análisis típico de la mecánica clásica con la condición de cuantificación expresada en el cuarto postulado.
Según la física clásica la energía cinética del electrón en órbita viene dada por la expresión:
![]()
Puesto que de acuerdo con la ecuación (16.8 - Ver "Orbitas, niveles de energía y espectros"):
![]()
y según la propia definición de energía cinética:
Ec = ½·mₑ·v²
Por otra parte, la electrostática establece que la energía potencial Eₚ para el sistema de cargas protón-electrón viene dada por:
![]()
Siendo en ambas expresiones "K" la constante electrostática de coulomb, es la carga del electrón y "r" el radio de la órbita.
La energía total, suma de cinética y potencial, será, por tanto:
E = Ec + Eₚ
![]()
![]()
Pero "r", de acuerdo con el cuarto postulado, está cuantificado y toma los valores dados por la ecuación (16.10):
![]()
Que sustituida en la expresión de la energía E da como resultado:
![]()
Expresión de los posibles valores de la energía del electrón del átomo de hidrógeno según el modelo de Bohr.
Aplicación de las ecuaciones características del modelo de Bohr
Determinar el valor de la longitud de onda correspondiente a la onda de materia asociada al electrón de un átomo de hidrógeno:
a) cuando se mueve en la órbita correspondiente al estado fundamental;
b) cuando lo hace en una órbita definida por el número cuántico n = 3.
Solución
a)
El estado fundamental de un electrón es el estado de más baja energía. Dado que en el modelo de Bohr la energía varía con el número cuántico "n" según la ecuación Eₙ = -E₀/n₂, el estado de más baja energía es el que corresponde a n = 1. La ecuación rₙ = a₀·n₂ indica que para n = 1, rₙ = a₀ = 5,29·10⁻¹¹ m. Luego, de acuerdo con la condición de Louis-Victor de Broglie:
2·π·rₙ = n·λ
Resulta:
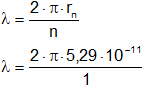
λ = 3,32·10⁻¹⁰ m = 3,32 Å
b)
Repitiendo el razonamiento anterior para n = 3 se tiene:
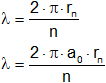
λ = 2·π·a₀·n
Sustituyendo resulta:
λ = 2·π·5,29·10⁻¹¹·3 = 9,96·10⁻¹¹ m = 9,96 Å
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).