Problema nº 1 de composición atómica, relación entre el volumen del átomo y el del núcleo - TP02

Enunciado del ejercicio nº 1

El radio aproximado del átomo de hidrógeno es de 0,0529 nm y el del protón es de 1,50·10⁻⁶ nm. Calcular la relación entre el volumen del átomo y el del núcleo, suponiendo a ambos esféricos.

Dato: volumen de la esfera = 4/3·π·r³

Desarrollo

Datos:

rₐ = 0,0529 nm

rₚ = 1,50·10⁻⁶ nm

Fórmulas:

Solución

Nos pide la siguiente relación:

Reemplazamos por la fórmula de volumen:

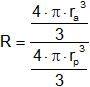
Simplificamos:

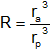
Reemplazamos por los datos y calculamos:

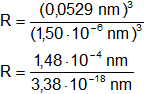
Respuesta, la relación entre el volumen del átomo y el del núcleo es:

R = 4,39·10¹³

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP02
• | Siguiente ›

Ejemplo, cómo determinar la relación entre el volumen del átomo y el del núcleo