Cambio espontáneo
Entropía
Las reacciones muy exotérmicas tienden a realizarse espontáneamente.
Reacción exotérmica: ΔH < 0
Reacción endotérmica: ΔH > 0
Sin embargo, las reacciones débilmente exotérmicas y endotérmicas también ocurren espontáneamente. No obstante, en ocasiones requieren de condiciones de reacción enérgicas. Por ejemplo, ocurren si se aumenta la temperatura.
Considérese la reacción de vapor de agua sobre carbón al rojo para formar monóxido de carbono e hidrógeno.
C + H₂O + energía ⟶ H₂ + CO
Los productos poseen mayor contenido de calor que los reactantes. Por tanto, como en este proceso se consume calor, ΔH es positivo.
Se ha determinado experimentalmente, que, si un mol de carbón reacciona con un mol de vapor de agua, entonces, ΔH = 31,4 kcal (como en la reacción precedente).
Se ha observado que la mayoría de las reacciones espontáneas parecen tener un ΔH < 0. En esta reacción ΔH > 0, se debe a un nuevo concepto.
Este nuevo concepto es la entropía o, desorden. En los sólidos cristalinos existe una distribución de los átomos muy ordenada. En los líquidos existe menos orden. En los gases no hay orden. Al grado de desorden se lo llama entropía. Se representa con el símbolo S.
La entropía S es una medida del desorden de un sistema.
Al cambio de entropía se lo simboliza por ΔS. Un valor positivo de ΔS indica disminución del grado de distribución ordenada. Este cambio (ΔS > 0) ocurre cuando un sólido se convierte en líquido o gas. Cuando ocurre la reacción opuesta, el líquido o gas se convierten en sólido, resulta ΔS < 0.
ΔS > 0 ⇒ incremento del desorden.
ΔS < 0 ⇒ incremento del orden.
Energía libre
El efecto combinado de ΔH y ΔS se llama energía libre. Su símbolo es G y ΔG representa la variación de la energía libre. La relación se expresa:
ΔG = ΔH - T·ΔS
Donde T es la temperatura absoluta (medida en Kelvin) a la que ocurre la reacción.
Puede demostrarse, teórica y experimentalmente, que, en un cambio espontáneo, ΔG siempre es negativo.
ΔG < 0 ⇒ cambio espontáneo.
Si una reacción ocurre a baja temperatura e involucra un ligero cambio de entropía, entonces, el término T·ΔS es despreciable. En esta reacción ΔG es prácticamente una función de ΔH, el cambio de entalpía. Por lo tanto, la mayoría de las reacciones que se efectúan a temperatura ambiente tienen ΔH < 0.
Las reacciones endotérmicas ocurren cuando T·ΔS es grande.
Esto significa que la temperatura es muy elevada o se presenta un gran incremento de la entropía.
En el ejemplo de la reacción endotérmica del carbón con vapor de agua, se tenían ambas condiciones. ΔS es positivo, pues, la distribución ordenada del carbón sólido se convierte en una distribución desordenada del monóxido de carbono.
La temperatura T es elevada puesto que la reacción únicamente ocurre al rojo (600 °C - 900 °C) o a mayor temperatura. Si la temperatura disminuye, la reacción cesa y, de hecho, se invierte.
Si ΔH y ΔS tienen el mismo signo, debe existir una temperatura en la cual ΔH y T·ΔS sean numéricamente iguales y ΔG será cero. Esta es la definición termodinámica de un sistema en equilibrio. En el equilibrio, el valor de la energía libre (en Física, no el de ΔG) es un mínimo para el sistema.
Todos los procesos espontáneos tienden al equilibrio. Por ejemplo, una pelota desciende por una colina, no asciende. La base de la colina es un lugar donde la pelota tiene la menor energía potencial. La energía potencial química, cuyo nombre técnico es energía libre, es mínima cuando un sistema se encuentra en equilibrio.
En el equilibrio: ΔG = 0
La consecuencia interesante de la contribución entrópica a la ecuación de la energía libre es que moléculas como H₂, O₂ y N₂, estables en la Tierra, no existen en el Sol ni en las estrellas.
Por ejemplo, la descomposición de un mol de moléculas de nitrógeno requiere una gran cantidad de energía.
N₂ + energía ⟶ 2·N
Energía = ΔH = 225 kcal (positiva)
Como ΔH tiene un valor positivo muy grande, a temperaturas ordinarias el N₂ es una molécula muy estable. Esto es una consecuencia directa de que T·ΔS es muy pequeño en comparación con el valor positivo tan grande ΔH, que hace positivo a ΔG. Si:
ΔH > T·ΔS ⇒ ΔG > 0 ⇒ cambio inducido.
ΔH < T·ΔS ⇒ ΔG < 0 ⇒ cambio espontáneo.
ΔH = T·ΔS ⇒ ΔG = 0 ⇒ en equilibrio.
Un gas constituido por átomos de nitrógeno tiene mayor entropía que uno formado por moléculas de nitrógeno.
Cálculos en base a la energía libre
Estados normales
Los parámetros de entalpía, entropía y energía libre dependen de la temperatura. Por tanto, se establecieron condiciones normalizadas para medir dichos parámetros, estos son: 298 K y 760 mm Hg. Se especifica la presión porque en algunas reacciones los parámetros también dependen de la presión.
Cálculos
Se sabe que el cambio de entalpía de una reacción se obtiene por la expresión:
ΔHₜ° = ΔHₚ° - ΔHᵣ°
Dónde:
ΔHₜ°: variación de la entalpía de la reacción.
ΔHₚ°: variación de la entalpía de los productos.
ΔHᵣ°: variación de la entalpía de los reactantes.
De forma semejante, los cambios de energía libre y entropía pueden calcularse para una reacción:
ΔGₜ° = ΔGₚ° - ΔGᵣ°
ΔSₜ° = ΔSₚ° - ΔSᵣ°
Ejemplo nº 1
¿Cuál es el cambio de entropía de la reacción entre el metano y el oxígeno en condiciones normales de medición?
CH₄ + 2·O₂ ⟶ CO₂ + 2·H₂O
Datos:
| Parámetro | CH₄ | O₂ | CO₂ | H₂O |
|---|---|---|---|---|
| ΔGf° (kcal/mol) | -12,13 | 0 | -94,258 | -56,688 |
| ΔHf° (kcal/mol) | -17,88 | 0 | -94,051 | -68,315 |
| S° (kcal/K) | 44,492 | 48,996 | 51,06 | 16,71 |
T = 298 K
Solución
Cálculo de ΔG°:
ΔGₜ° = ΔGₚ° - ΔGᵣ°
Reemplazamos por los valores y calculamos:
ΔGₜ° = [-94,258 + 2·(-56,688)] - (-12,13 + 2·0)
ΔGₜ° = (-94,258 - 113,376) - (-12,13)
ΔGₜ° = -207,634 + 12,13
ΔGₜ° = -195,504 kcal/mol
Cálculo de ΔH°:
ΔHₜ° = ΔHₚ° - ΔHᵣ°
Reemplazamos por los valores y calculamos:
ΔHₜ° = [-94,051 + 2·(-68,315)] - (-17,88 + 2·0)
ΔHₜ° = (-94,051 - 136,63) - (-17,88)
ΔHₜ° = -230,681 + 17,88
ΔHₜ° = -212,801 kcal/mol
Cálculo de ΔS°:
ΔSₜ° = ΔSₚ° - ΔSᵣ°
Reemplazamos por los valores y calculamos:
ΔSₜ° = (51,06 + 2·19,71) - (44,492 + 2·48,996)
ΔSₜ° = (51,06 + 33,42) - (44,492 + 97,992)
ΔSₜ° = 84,48 - 142,484
ΔSₜ° = -58,004 cal/K
Calcularemos la variación de la entropía con la fórmula de la energía libre:
ΔG = ΔH - T·ΔS
Despejamos ΔS:
![]()
Reemplazamos por los datos y calculamos:
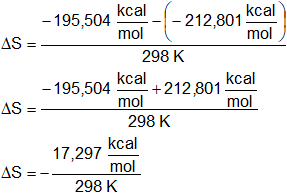
ΔS = -0,058004 kcal/K = -58,004 cal/K
Estas ecuaciones termodinámicas permiten determinar con mucha precisión la posible dirección de un sistema reaccionante.
Ejemplo nº 2
¿Cuál es la entropía normal del sulfuro bismutoso?
2·Bi + 3·S ⟶ Bi₂S₃
Fórmula:
ΔG = ΔH - T·ΔS
Datos:
| Parámetro | Bi | S | Bi₂S₃ |
|---|---|---|---|
| ΔGf° (kcal/mol) | 0 | 0 | -33,6 |
| ΔHf° (kcal/mol) | 0 | 0 | -34,2 |
| S° (kcal/K) | 13,56 | 7,6 | x |
T = 298 K
Solución
Cálculo de ΔG°:
ΔGₜ° = ΔGₚ° - ΔGᵣ°
Reemplazamos por los valores y calculamos:
ΔGₜ° = -33,6 - (2·0 + 3·0)
ΔGₜ° = -33,6 kcal/mol
Cálculo de ΔH°:
ΔHₜ° = ΔHₚ° - ΔHᵣ°
Reemplazamos por los valores y calculamos:
ΔHₜ° = -34,2 - (2·0 + 3·0)
ΔHₜ° = -34,2 kcal/mol
Cálculo de ΔS°:
ΔG = ΔH - T·ΔS
Despejamos ΔS:
![]()
Reemplazamos por los datos y calculamos:
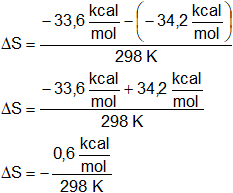
ΔS = -0,00201 kcal/K = -2,01 cal/K
Para obtener ΔSBj₂S₃°:
ΔSₜ° = SBj₂S₃° - (2·SBi° + 3·SS°)
SBj₂S₃° = ΔSₜ° + 2·SBi° + 3·SS°
Reemplazamos por los valores y calculamos:
Sₜ° = -2,01 + 2·13,56 + 2·7,6
Sₜ° = -2,01 + 27,12 + 22,8
Sₜ° = 47,92 cal/K
Bibliografía:
Héctor Fernández Serventi. "Química general e inorgánica". Losada S. A., Buenos Aires.
Robert C. Smoot y Jack Price. "Química, Un curso moderno". Compañía Editorial Continental S. A., México.
Autor: Ricardo Santiago Netto. Argentina
- ‹ Anterior
- |
- Siguiente ›