Leyes de la electrólisis

Los siguientes conceptos son referidos a la corriente eléctrica necesarios para comprender el significado de las leyes de Michael Faraday:

1) La cantidad de electrones (electricidad) que circulan por un conductor se mide en coulomb.

q = carga ⟶ [q] = coulomb

2) La intensidad de la corriente (caudal de electrones) expresa la cantidad de electricidad que circula por un conductor por unidad de tiempo. La intensidad de la corriente se mide en ampere.

q = i·t ⟶ [i] = (A)

3) Cuando una fuente fuerza a los electrones a circular por un conductor, se presenta una resistencia al flujo de corriente y se produce una caída de potencial. La resistencia eléctrica se mide en ohm, y la diferencia de potencial en volt.

E = i·R ⟶ [E] = (V) y [R] = ohm (Ω)

Leyes de Faraday

Primera Ley de Faraday

La masa de un elemento depositada en un electrodo es proporcional a la cantidad de electricidad que pasa a través de la solución del electrólito o del electrólito fundido.

m = ζ·i·t

Donde ζ es una constante que depende del catión y se denomina equivalente electroquímico (se verá más adelante).

Cuando se realiza, por ejemplo, la electrólisis de una solución de sulfato cúprico (CuSO₄) sucede lo siguiente (figura 1):

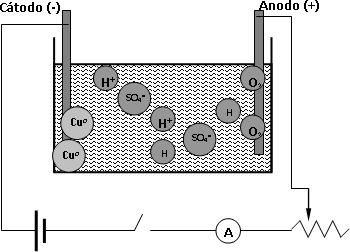
Figura 1: Electrólisis del sulfato cúprico y la primera ley de Faraday

Cu₂SO₄ + H₂O ⟶ Cu²⁺ + SO₄⁼ + H⁺ + HO⁻

Al aplicar una diferencia de potencial a los electrodos, el ion cobre se mueve hacia el cátodo, adquiere dos electrones y se deposita en el electrodo como elemento cobre. El ion sulfato, al descargarse en el electrodo positivo, es inestable y se combina con el agua de la disolución formando ácido sulfúrico y oxígeno.

2·Cu²⁺ ⟶ 2·Cu ° - 4·e⁻

2·HO⁻ ⟶ O₂ + 2·H⁺ + 4·e⁻

2·Cu₂SO₄ + 2·H₂O ⟶ 2·Cu ° + 2·H₂SO₄ + O₂

Cuando circula más corriente (más coulombios) más cobre se deposita, pues más electrones han circulado permitiendo que más iones cobre (Cu²⁺) se conviertan en elemento cobre (Cu°).

Ejemplo:

Una corriente de 15 A fluye durante 10.000 s. ¿Qué masa de Ni³⁺ se deposita?

Aplicamos la primera ley de Faraday:

m = ζ·i·t

Reemplazamos por los datos y calculamos:

m = 0,000203 g/C·15 A·10.000 s

m = 30,45 g

Segunda Ley de Faraday

Las masas de los elementos que se depositan en los electrodos son proporcionales a los equivalentes químicos.

Recordemos que el equivalente químico de un elemento es el cociente entre el peso atómico gramo de ese elemento y su valencia:

Para probar esta segunda ley se hace pasar la misma cantidad de electricidad a través de varias cubas con diferentes soluciones salinas, como indica la figura. Midiendo la cantidad de plata y de cobre depositados en el cátodo se llega a la comprobación de la ley:

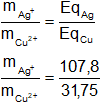
O sea que las masas de plata y de cobre depositadas en los electrodos se hallan en relación de: 107,8/31,75.

Figura 2: Electrólisis en serie del sulfato cúprico y el nitrato de plata, segunda ley de Faraday

Número de Faraday

Para depositar el equivalente químico de cualquier elemento se necesita la misma cantidad de electricidad. La constante o número de faradio (F) es de 96.500 coulomb (96.494 C).

F = e·N_A

Por ejemplo, para depositar: 1,008 g de H⁺, 107,8 g de Ag⁺, 31,75 g de Cu²⁺ o 63,5 g de Cu⁺ son necesarios 96.500 coulomb.

Vale aclarar que: 96.500 coulomb = carga de 6,02·10²³ electrones, de lo que se deduce que la carga de un electrón es 1,6·10⁻¹⁹ coulomb.

Ejemplo:

Calcular el número de Faraday en culombios si la carga del electrón es de 1,602·10⁻¹⁹ C y el número de Avogadro es de 6,02·10²³.

Aplicamos la fórmula de Faraday:

F = e·N_A

Reemplazamos por los datos y calculamos:

F = 1,602·10⁻¹⁹ C·6,02·10²³

F = 96.601 C

Equivalente electroquímico

Se llama equivalente electroquímico ζ a la masa de un elemento depositada, durante la electrólisis, por la carga de un coulomb.

En todos los casos, la cantidad de material que se deposita en cada electrodo al pasar la corriente por un electrólito sigue las leyes de Faraday.

Todos los cambios químicos implican una reagrupación o reajuste de los electrones en las sustancias que reaccionan; por eso puede decirse que dichos cambios son de carácter eléctrico. Para producir una corriente eléctrica a partir de una reacción química, es necesario tener un oxidante, es decir, una sustancia que gane electrones fácilmente, y un reductor, es decir, una sustancia que pierda electrones fácilmente.

Ejemplo:

Calcular el equivalente electroquímico del hierro trivalente.

Primero calculamos el equivalente químico.

La masa atómica del Fe es 55,847 g

Cuando actúa con valencia 3:

Eq = 18,61566667 g

Aplicamos la fórmula de equivalente electroquímico:

ζ = 0,000193 g/C

Ecuación de Nernst

En condiciones normales, la diferencia de potencial de una celda es E°. Los valores de la tabla de potenciales de oxidación-reducción, son los valores de E° para soluciones molares a 25 °C y 1 atmósfera de presión.

Si se desea el voltaje de una celda en condiciones diferentes de las normales, puede utilizarse la ecuación de Nernst.

Donde:

R es la constante de los gases ideales.

Para aplicar R a cálculos eléctricos es necesario expresar sus unidades apropiadamente, así, la conversión en calorías por mol·K ≡ 1,99.

T es la temperatura en grados kelvin.

n es el número de electrones en la ecuación redox balanceada ocurrido en la celda.

F es un factor de conversión de volts a calorías cuyo valor es 23.100 (no confundir F con número de Faraday).

El logaritmo natural ln puede sustituirse por 2,30·log, para facilitar los cálculos.

El valor (R/F)·2,30 ≡ 1,98·10⁻⁴.

Si introducimos la temperatura normal de 25 °C como 298 K al factor anterior, se obtiene 0,0592.

La ecuación de Nernst puede escribirse:

Ejemplo:

¿Cuál sería el voltaje de una celda constituida por Ni/Ni²⁺ (2,50 M) y Ag/Ag⁺ (0,10 M) a temperatura y presión normales?

Ni°(s) + 2·Ag⁺(aq) ⟶ Ni²⁺(aq) + 2·Ag°(s)

El intercambio de electrones es 2 ⇒ n = 2.

De la tabla de potenciales de oxidación-reducción obtenemos los potenciales de cada par:

Ni²⁺ + 2·e ⟶ Ni° (-0,24 V)

Ag⁺ + e ⟶ Ag° (0,8 V)

E° = 0,8 V - (-0,24 V)

E° = 0,8 V + 0,24 V

E° = 1,04 V

Reemplazamos en la ecuación de Nernst y calculamos:

E = 1,04 V - 0,0296 V·log 250

E = 1,04 V - 0,0296 V·2,40

E = 1,04 V - 0,07 V

E = 0,97 V

Bibliografía:

Robert C. Smoot y Jack Price. "Química, Un curso moderno". Compañía Editorial Continental S. A., México.

Autor: Ricardo Santiago Netto. Argentina

¿Que postula la ley de Faraday?