Problema nº 5 de electrólisis. Concentración y ka dada la constante de ionización - TP05

Enunciado del ejercicio nº 5

¿Cuál es la concentración del ion hidronio de una solución de KHSO₄ 0,1 M? Consulte el valor de kₐ en la tabla de constantes de ionización.

Solución

Expresamos la ecuación balanceada de disociación:

KHSO₄ + H₂O ⇌ H₃O⁺ + KSO₄⁻

Planteamos los moles iniciales y en el equilibrio:

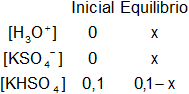
Aplicamos la constante de equilibrio para un ácido (kₐ):

Reemplazamos por los datos:

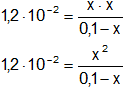
1,20·10⁻²·(0,1 - x) = x²

Igualamos a cero:

x² - 1,20·10⁻²·(0,1 - x) = 0

Aplicamos distributiva del producto con respecto a la resta:

x² + 1,20·10⁻²·x - 1,20·10⁻³ = 0

x² + 0,012·x - 0,0012 = 0

Aplicamos la ecuación de Báscara o Bhaskara:

Siendo:

a = 1

b = 0,012

c = -0,0012

Reemplazamos y resolvemos, obtendremos dos valores:

Calculamos los valores de x_1,2 por separado según el signo del resultado de la raíz:

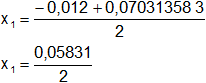
x₁ = 2,92·10⁻² mol/l

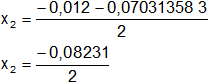
x₂ = -4,12·10⁻² mol/l (se descarta por < 0)

Respuesta: la concentración del ion hidronio de una solución de KHSO₄ 0,1 M es 2,9·10⁻² mol/l.

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP05
• | Siguiente ›

Ejemplo, cómo calcular la concentración dada la constante de ionización