Problema nº 3, constante de equilibrio químico - TP03
Enunciado del ejercicio nº 3
Un mol de alcohol etílico puro se mezcla con un mol de ácido acético puro a temperatura ambiente. La mezcla, en equilibrio, contiene: ⅔ de mol de etanoato de etilo y ⅔ de mol de agua.
a) Calcular la constante de equilibrio.
b) ¿Cuántos moles de etanoato de etilo hay en el equilibrio cuando se mezclan 3 moles de alcohol etílico con un mol de ácido acético?
Todas las sustancias son líquidas a la temperatura de reacción.
Solución
Expresamos la ecuación equilibrada de la reacción:
CH₃CH₂OH + CH₃COOH ⇌ CH₃COOCH₂CH₃ + H₂O
a)
Planteamos los moles iniciales y en el equilibrio:
| Inicial | Equilibrio | |
|---|---|---|
| [CH₃COOCH₂CH₃] | 0 | ⅔ |
| [H₂O] | 0 | ⅔ |
| [CH₃CH₂OH] | 1 mol | 1 - ⅔ |
| [CH₃COOH] | 1 mol | 1 - ⅔ |
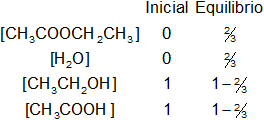
Aplicamos la fórmula de la constante de equilibrio:
Suponemos que el volumen es constante, por lo tanto, las concentraciones en todos los casos quedan indicados por los valores absolutos de moles de cada sustancia.
Reemplazamos por los datos y calculamos:
Simplificamos:
K = 4
Respuesta a): el valor de la constante de equilibrio K es 4.
b)
x será el número de moles de etanoato de etilo y de agua en el equilibrio.
Si se forman x moles de etanoato de etilo y x moles de agua, desaparecen x moles de alcohol etílico y x moles de ácido acético.
Planteamos los moles iniciales y en el equilibrio:
| Inicial | Equilibrio | |
|---|---|---|
| [CH₃COOCH₂CH₃] | 0 | x |
| [H₂O] | 0 | x |
| [CH₃CH₂OH] | 3 mol | 1 - x |
| [CH₃COOH] | 1 mol | 1 - x |
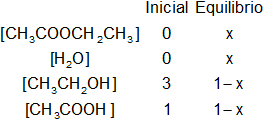
Aplicamos la fórmula de la constante de equilibrio:
Reemplazamos:
Suponemos que el volumen es constante, por lo tanto, las concentraciones en todos los casos quedan indicados por los valores absolutos de moles de cada sustancia.
Aplicamos distributiva del producto con respecto a la resta:
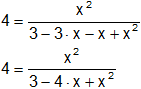
4·(3 - 4·x + x²) = x²
12 - 16·x + 4·x² = x²
Igualamos a cero:
4·x² - x² - 16·x + 12 = 0
3·x² - 16·x + 12 = 0
Aplicamos la ecuación de Báscara o Bhaskara:
Siendo:
a = 3
b = -16
c = 12
Reemplazamos y resolvemos, obtendremos dos valores:
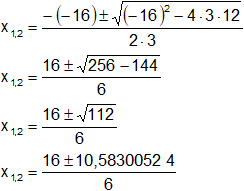
Calculamos los valores de x1,2 por separado según el signo del resultado de la raíz:
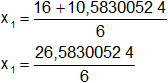
x₁ = 4,430500874 moles de etanoato de etilo (se descarta porque no puede haber más de 1 mol de etanoato de etilo partiendo de 1 mol de ácido acético)
x₂ = 0,902832459 moles de etanoato de etilo
Respuesta b): la cantidad de moles de etanoato de etilo que hay en el equilibrio es 0,9.
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP03
- | Siguiente ›
Ejemplo, cómo calcular la constante de equilibrio