Problema nº 4 de equilibrio químico, las presiones parciales y los moles - TP03

Enunciado del ejercicio nº 4

En un recipiente de 10 litros se hace reaccionar a 448 °C, 0,5 moles de H₂ y 0,5 moles de I₂.

H₂(g) + I₂(g) ⟶ 2·HI(g)

Calcular:

a) El valor de kₚ.

b) ¿Cuál es la presión total en el recipiente?

c) ¿Cuántos moles de yodo quedan sin reaccionar en el equilibrio?

d) ¿Cuál es la presión parcial de cada compuesto en la mezcla en el equilibrio?

Desarrollo

Datos:

K = 50

Moles _H = 0,5

Moles _I = 0,5

V = 10 l

Solución

a)

Como el volumen del recipiente se mantiene constante, las concentraciones en todos los casos quedan indicados por los valores absolutos de moles de cada sustancia.

Los reactantes y los productos son gases y, en ambos lados de la ecuación existe la misma cantidad de moles y volúmenes, por lo tanto, la reacción no se vería afectada por un cambio de presión o de volumen, entonces, Kₚ = K = 50.

Expresamos la ecuación equilibrada de la reacción:

H₂(g) + I₂(g) ⟶ 2·HI(g)

Demostración:

Aplicamos la fórmula de la constante de equilibrio:

Desarrollamos:

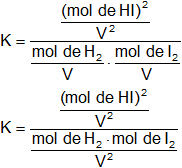
Simplificamos los denominadores:

(1)

Aplicamos la fórmula de la constante de equilibrio de presiones parciales:

Desarrollamos:

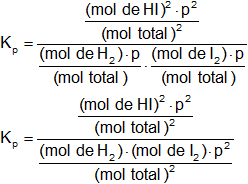
Simplificamos:

Como vemos, las ecuaciones (1) y (2) son iguales, por lo tanto:

Kₚ = K = 50

Respuesta a): la constante de equilibrio de presiones parciales Kₚ = 50.

b)

Antes, durante y luego de la reacción, el número total de moles permanece constante:

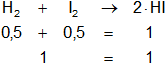
El número total de moles es 1 (n = 1)

Aplicamos la ecuación de estado de los gases:

p·V = n·R·T

Despejamos la presión P:

Adecuamos la temperatura:

T = 448 °C + 273 °C = 721 K

Reemplazamos por los datos:

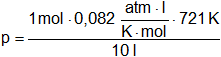
Resolvemos:

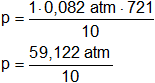
P = 5,9122 atm

Respuesta b): la presión total en el recipiente es 5,9 atm.

c)

Planteamos los moles iniciales y en el equilibrio:

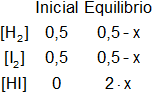
x es el número de moles de cada componente en el equilibrio.

Si se forman x moles de HI, desaparecen x moles de yodo y x moles de hidrógeno.

Aplicamos la fórmula de la constante de equilibrio:

Reemplazamos por los datos y calculamos:

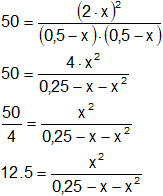
12,5·(0,25 - x + x²) = x²

Aplicamos distributiva del producto con respecto a la resta:

12,5·x² - 12,5·x + 3,125 = x²

Igualamos a cero:

12,5·x² - x² - 12,5·x + 3,125 = 0

11,5·x² - 12,5·x + 3,125 = 0

Aplicamos la ecuación de Báscara o Bhaskara:

Siendo:

a = 11,5

b = -12,5

c = 3,125

Reemplazamos y resolvemos, obtendremos dos valores:

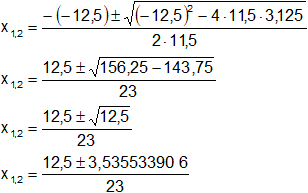
Calculamos los valores de x_1,2 por separado según el signo del resultado de la raíz:

x₁ = 0,697197126 (se descarta porque no puede haber más de 0,5 moles de cada reactante)

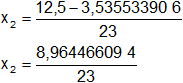
x₂ = 0,389759395

Por lo tanto:

x = 0,389759395

Los moles de yodo en el equilibrio será:

[I₂] = 0,5 - 0,389759395

[I₂] = 0,110240605

Respuesta c): la cantidad de moles de yodo que hay en el equilibrio es 0,11.

d)

Aplicamos la fórmula de presión parcial:

Reemplazamos por los datos y calculamos:

p_H2 = 0,651764503 atm

Reemplazamos por los datos y calculamos:

p_I2 = 0,651764503 atm

p_HI = p - (p_H2 + p_I2)

Reemplazamos por los datos y calculamos:

p_HI = 5,9122 atm - (0,651764503 atm + 0,651764503 atm)

p_HI = 5,9122 atm - 1,303529005 atm

p_HI = 4,608670995 atm

Resultado d):

p_H2 = 0,65 atm

p_I2 = 0,65 atm

p_HI = 4,61 atm

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP03
• | Siguiente ›

Ejemplo, cómo calcular la constante de equilibrio, las presiones parciales y los moles