Problema nº 7 de electrólisis. Leyes de Faraday y equivalente electroquímico, masa que se deposita en el cátodo y la carga - TP02

Enunciado del ejercicio nº 7

¿Durante cuánto tiempo deberá circular una corriente de 2 A por una solución de cloruro cúprico para conseguir un depósito de 70 g de cobre?

¿Qué cantidad de corriente circuló durante ese tiempo?

Siendo F = 96.500 C y P.A. del cobre 63,5; hallar su equivalente electroquímico.

i = 2 A

m _Cu = 70 g

P.A. _Cu = 63,5 g

F = 96.500 C

ζ_Cu²⁺ = 0,000329 g/C *

m = ζ·i·t

ζ =	Eq
	F

a) Cálculo del tiempo empleado.

Aplicamos la primera ley de Faraday:

m = ζ·i·t

Despejamos t:

t =	m
	ζ·i

Reemplazamos por los datos y calculamos:

t =	70 g
	0,000329 g/C·2 A

t =	70 C
	0,000658 A

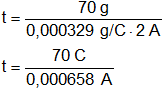
Recordemos que C/s = A.

t = 106.382,9787 s

Respuesta a): el tiempo requerido es de 106.383 s (29 h 33 min 2 s).

b) Cálculo de la carga.

Aplicamos la fórmula de carga eléctrica:

q = i·t

Reemplazamos por los datos y calculamos:

q = 2 A·106.382,9787 s

q = 212.765,9574 C

Respuesta b): carga total es 212.766 C.

c) Cálculo del equivalente electroquímico.

Hallamos el equivalente químico del cobre bivalente:

Eq =	P.A.
	V

Reemplazamos por los datos y calculamos:

Eq =	63,5 g
	2

Eq = 31,75 g

Aplicamos la fórmula del equivalente electroquímico:

ζ =	Eq
	F

Reemplazamos por los datos y calculamos:

ζ =	31,75 g
	96.500 C

ζ = 0,000329016 g/C

Respuesta c): el equivalente electroquímico es 0,000329 g/C.

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular la masa que se deposita en el cátodo y la carga