Problema nº 7 de equilibrio químico, moles - TP03

Enunciado del ejercicio nº 7

Se tiene:

H₂(g) + I₂(g) ⟶ 2·HI(g)

Si se calientan 46 g de I₂ y 1,0 g de H₂ hasta el equilibrio a 450 °C, la mezcla en el equilibrio contiene 1,9 g de I₂.

Calcular:

a) ¿Cuántos moles de cada gas hay en la mezcla en el equilibrio?

b) Calcular la constante de equilibrio.

Solución

Expresamos la ecuación equilibrada de la reacción:

Supondremos que la reacción ocurre en un recipiente a volumen constante.

Hallamos los pesos moleculares de las sustancias:

Mol _H₂ = 2·1,00797 = 2,01594 g

Mol _I₂ = 2·126,9044 = 253,8088 g

Mol _HI = 1,00797 + 126,9044 = 127,91237 g

Estequiométricamente:

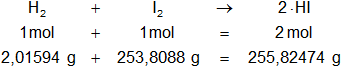
x = 125,9009693 g de I₂

Para que reaccione 1 gramo de hidrógeno hace falta 125,9 gramos de yodo, pero, solo hay 46 gramos de yodo. El yodo es el reactivo limitante.

En una reacción completa, suponiendo un rendimiento del 100 %:

x = 0,365366528 g de H₂

Esto nos dice que 0,634633472 g de H₂ no reaccionan con un rendimiento del 100 %. Pero el enunciado dice que en el equilibrio hay 1,9 g de yodo, calculemos la cantidad de hidrógeno que reacciona:

Masa de yodo = 46 g - 1,9 g = 44,1 g

x = 0,350275302 g de H₂

Lo expresamos en los cálculos estequiométricos:

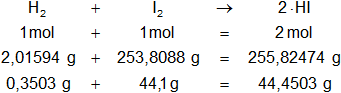
La masa de hidrógeno que no reacciona es:

1 g - 0,350275302 g = 0,649724698 g de H₂

A continuación, hallamos los moles que intervienen:

x = 0,322293669 moles de H₂ ≅ 0,3223 moles de H₂ en el equilibrio

x = 0,00748595 moles de I₂ ≅ 0,0075 moles de I₂ en el equilibrio

x = 0,347505681 mol de HI ≅ 0,3475 moles de HI en el equilibrio

Planteamos los moles iniciales y en el equilibrio:

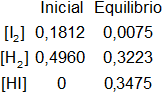
Aplicamos la fórmula de la constante de equilibrio:

Reemplazamos por los datos y calculamos:

K = 50,05242454

Respuesta: el valor de la constante de equilibrio K es 50.

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP03
• | Siguiente ›

Ejemplo, cómo calcular la constante de equilibrio y los moles