Problema nº 10 de gases ideales, masa y moléculas de un gas - TP03

Enunciado del ejercicio nº 10

En un recipiente hay 12 litros de cloro a 304 mm Hg y 0 °C de temperatura, calcular:

a) Masa de cloro.

b) Número de moléculas.

c) Cantidad de átomos.

Desarrollo

Datos:

V = 12 l

p = 304 mm Hg

t = 0 °C

Fórmulas:

p·V·mol = m·R·T

Solución

Convertimos las unidades:

V = 12 l = 12 dm³

T = 0 °C = 273 K

p = 0,4 atm

Calculamos la masa de un mol de cloro gaseoso:

PM Cl₂: 2·35,453 g = 70,906 g

a)

Aplicamos la ecuación estado de los gases ideales para determinar la masa de cloro, despejamos "m":

Reemplazamos por los datos y calculamos:

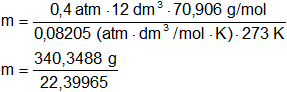
Resultado, la masa de cloro es:

m = 15,19 g

b)

Calculamos las moléculas de cloro (Cl₂) en las condiciones dadas:

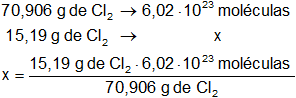
Resultado, las moléculas de cloro son:

x = 1,29·10²³ moléculas de Cl₂

c)

Calculamos los átomos de cloro en las condiciones dadas, su molécula es biatómica:

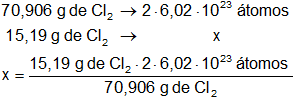
Resultado, los átomos de cloro son:

x = 2,58·10²³ átomos

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP03
• | Siguiente ›

Ejemplo, cómo calcular la masa y moléculas de un gas