Problema nº 6 de electrólisis. Concentración dada la constante de ionización - TP03

Enunciado del ejercicio nº 6

Calcular la concentración del ion hidrógeno en las siguientes soluciones:

a) Solución 0,5 molar de HF (Kₐ = 6,8·10⁻⁴)

b) Solución 0,6 molar de HNO₂ (Kₐ = 4,6·10⁻³)

Desarrollo

La concentración de iones [H⁺] o de iones [OH⁻] de un ácido o de una base totalmente disociados coincide con la normalidad de la solución.

Solución

Expresamos la ecuación balanceada de disociación:

HF ⇌ H⁺ + F⁻

Planteamos los moles iniciales y en el equilibrio:

	Inicial	Equilibrio
[H⁺]	0	x
[F⁻]	0	x
[HF]	0,5 moles	0,5 - x

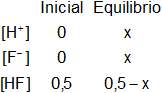
Aplicamos la constante de equilibrio para un ácido (kₐ):

kₐ =	[H⁺]·[F⁻]
	[HF]

Reemplazamos por los datos:

6,8·10⁻⁴ =	x·x
	0,5 - x

6,8·10⁻⁴ =	x²
	0,5 - x

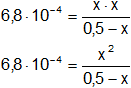
6,8·10⁻⁴·(0,5 - x) = x²

Igualamos a cero:

x² - 6,8·10⁻⁴·(0,5 - x) = 0

Aplicamos distributiva del producto con respecto a la resta:

x² + 0,00068·x - 0,00034 = 0

Aplicamos la ecuación de Báscara o Bhaskara:

x_1,2 =	-b ± √b² - 4·a·c
	2·a

Siendo:

a = 1

b = 0,00068

c = -0,00034

Reemplazamos y resolvemos, obtendremos dos valores:

x_1,2 =	-0,00068 ± √0,00068² - 4·1·(-0,00034)
	2·1

x_1,2 =	-0,00068 ± √0,0013604624
	2

x_1,2 =	-0,00068 ± 0,036884447
	2

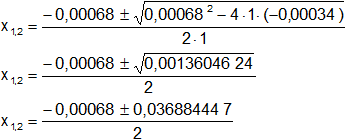
Calculamos los valores de x_1,2 por separado según el signo del resultado de la raíz:

x₁ =	-0,00068 + 0,036884447
	2

x₁ =	0,03620
	2

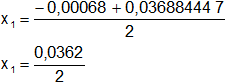
x₁ = 1,81·10⁻² mol/l

x₂ =	-0,00068 - 0,036884447
	2

x₂ =	-0,03756
	2

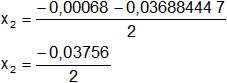
x₂ = -1,88·10⁻² mol/l (se descarta por < 0)

Respuesta a): la concentración del ion hidrógeno en la solución 0,5 molar de HF es 1,8·10⁻² mol/l.

Expresamos la ecuación balanceada de disociación:

HNO₂ ⇌ H⁺ + NO₂⁻

Planteamos los moles iniciales y en el equilibrio:

	Inicial	Equilibrio
[H⁺]	0	x
[NO₂⁻]	0	x
[HNO₂]	0,6 moles	0,6 - x

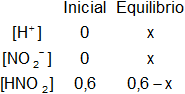
Aplicamos la constante de equilibrio para un ácido (kₐ):

kₐ =	[H⁺]·[NO₂⁻]
	[HNO₂]

Reemplazamos por los datos:

4,6·10⁻⁴ =	x·x
	0,6 - x

4,6·10⁻⁴ =	x²
	0,6 - x

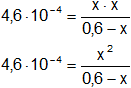
4,6·10⁻⁴·(0,6 - x) = x²

Igualamos a cero:

x² - 4,6·10⁻⁴·(0,6 - x) = 0

Aplicamos distributiva del producto con respecto a la resta:

x² + 0,00046·x - 0,000276 = 0

Aplicamos la ecuación de Báscara o Bhaskara:

x_1,2 =	-b ± √b² - 4·a·c
	2·a

Siendo:

a = 1

b = 0,00046

c = -0,000276

Reemplazamos y resolvemos, obtendremos dos valores:

x_1,2 =	-0,00046 ± √0,00046² - 4·1·(-0,000276)
	2·1

x_1,2 =	-0,00046 ± √0,0011042116
	2

x_1,2 =	-0,00046 ± 0,03322968
	2

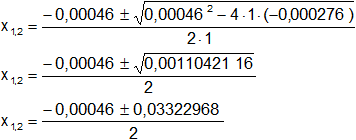
Calculamos los valores de x_1,2 por separado según el signo del resultado de la raíz:

x₁ =	-0,00046 + 0,03322968
	2

x₁ =	0,03277
	2

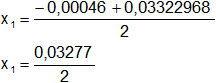
x₁ = 1,64·10⁻² mol/l

x₂ =	-0,00046 - 0,03322968
	2

x₂ =	-0,03369
	2

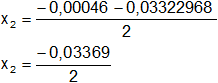
x₂ = -1,68·10⁻² mol/l (se descarta por < 0)

Respuesta b): la concentración del ion hidrógeno en la solución 0,6 molar de HNO₂ es 1,6·10⁻² mol/l.

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular la concentración dada la constante de ionización