Problema nº 3, constante de equilibrio químico, moles (ejercicio modelo) - TP01

Enunciado del ejercicio nº 3

Siendo a 425 °C la constante de equilibrio para el yoduro de hidrógeno, tal como en el ejercicio nº 1, si se colocan 0,018 moles de yoduro de hidrógeno en un recipiente de 10 litros, ¿cuántos moles de yodo habrá en equilibrio?

Desarrollo

Datos:

K = 0,0184

Moles _HI = 0,018

V = 10 l

Solución

Expresamos la ecuación equilibrada de la reacción:

x será el número de moles de yodo y de hidrógeno en el equilibrio.

Si se forman x moles de hidrógeno y x moles de yodo, desaparecen 2·x moles de yoduro de hidrógeno.

Calculamos la concentración de cada compuesto en 10 l. Para el yodo:

Para el hidrógeno:

Para el yoduro de hidrógeno:

Aplicamos la fórmula de la constante de equilibrio:

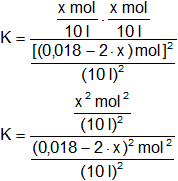
Cálculo de la constante de equilibrio

Simplificamos los denominadores y las unidades:

Reemplazamos por los datos y calculamos:

0,0184·(0,018 - 2·x)² = x²

0,0184·[(0,018² - 2·0,018·2·x + (2·x)²] = x²

0,0184·(0,000324 - 0,072·x + 4·x²) = x²

0,000005962 - 0,0013248·x + 0,0736·x² = x²

0,000005962 - 0,0013248·x + 0,0736·x² - x² = 0

0,000005962 - 0,0013248·x - 0,9264·x² = 0

Resolvemos la ecuación de segundo grado y obtenemos dos valores para x:

x₁ = -0,00335 moles < 0, se descarta

x₂ = 0,0019 moles

Respuesta: la cantidad de moles de yodo que hay en el sistema es 0,002

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular los moles dada la constante de equilibrio