Problema nº 10 de equilibrio químico, presiones parciales, moles y presiones parciales de una mezcla de gases - TP03

Enunciado del ejercicio nº 10

Se tiene:

CO(g) + H₂O(g) ⇌ CO₂(g) + H₂(g)

La constante de equilibrio para esta reacción a 986 °C es 0,63. Se mezcla en un recipiente un mol de vapor de agua y tres moles de monóxido de carbono alcanzando el equilibrio a una presión total de 2 atmósferas.

a) ¿Cuántos moles de H₂ hay en el equilibrio?

b) ¿Cuál es la presión parcial de cada gas en la mezcla en el equilibrio?

Desarrollo

Datos:

K = 0,63

p_T = 2 atm

Solución

Expresamos la ecuación equilibrada de la reacción:

a)

Planteamos los moles iniciales y en el equilibrio:

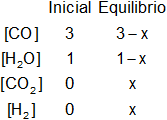
x será el número de moles de CO₂ y H₂ en el equilibrio.

En el equilibrio desaparecen x moles de CO y de H₂O para formar x moles de CO₂ y H₂.

Aplicamos la fórmula de la constante de equilibrio:

Reemplazamos por los datos y calculamos:

Aplicamos distributiva del producto con respecto a la resta:

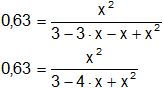
Pasamos de término:

0,63·(x² - 4·x + 3) = x²

0,63·x² - 0,63·4·x + 0,63·3 = x²

0,63·x² - 2,52·x + 1,89 = x²

Igualamos a cero:

0,63·x² - x² - 2,52·x + 1,89 = 0

-0,37·x² - 2,52·x + 1,89 = 0

0,37·x² + 2,52·x - 1,89 = 0

Aplicamos la ecuación de Báscara o Bhaskara:

Siendo:

a = 0,37

b = 2,52

c = -1,89

Reemplazamos y resolvemos, obtendremos dos valores:

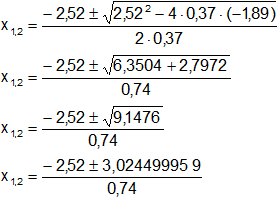
Calculamos los valores de x_1,2 por separado según el signo del resultado de la raíz:

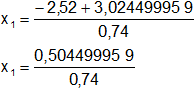
x₁ = 0,681756701

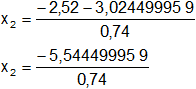
x₂ = -7,492567512 (se descarta por ser < 0)

Respuesta a): la cantidad de moles de H₂ que hay en el equilibrio es 0,68, es la misma cantidad de moles de CO₂.

b)

Del paso anterior sabemos que:

Mol_H2 = 0,681756701

Mol_CO2 = 0,681756701

Calculamos los moles de CO y de H₂O en el equilibrio:

Mol_CO = 3 - x = 3 - 0,681756701

Mol_CO = 2,318243299

Mol_H2O = 1 - x = 1 - 0,681756701

Mol_H2O = 0,318243299

Aplicamos la fórmula que relaciona las presiones parciales con la fracción molar (Ver Constante de equilibrio de las presiones parciales):

n_T = 4

Reemplazamos:

p_H2 = 0,34087835 atm.

p_CO2 = 0,34087835 atm.

p_CO = 1,15912165 atm.

p_H2O = 0,15912165 atm.

Respuesta b): la presión parcial de cada gas en la mezcla en el equilibrio son.

p_H2 = 0,34 atm.

p_CO2 = 0,34 atm.

p_CO = 1,16 atm.

p_H2O = 0,16 atm.

Podemos verificar aplicamos la fórmula de la constante de equilibrio de las presiones parciales:

Dado que no hay variación entre los volúmenes de reactantes y productos:

Kₚ = K

Reemplazamos:

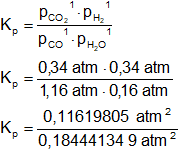
Kₚ = 0,63 ∎

También podemos verificar la p_T aplicando la ley de las presiones parciales de Dalton sabemos que:

p_T = ∑p_g

p_T = p_CO + p_H2O + p_CO2 + p_H2

Reemplazamos:

p_T = 1,15912165 atm + 0,15912165 atm + 0,34087835 atm + 0,34087835 atm

p_T = 2 atm ∎

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP03
• | Siguiente ›

Ejemplo, cómo calcular los moles y las presiones parciales de una mezcla de gases en el equilibrio