Problema nº 5-b de ecuaciones de óxido reducción, equilibrar por el método del ion electrón - TP01

Enunciado del ejercicio nº 5-b

Igualar la siguiente ecuación por el método del ion electrón:

KMnO₄ + HCl ⟶ KCl + MnCl₂ + H₂O + Cl₂

Reacción de oxidación del ácido clorhídrico por el ion permanganato con formación de cloruro de manganeso y cloro libre.

Primero disociamos los compuestos, detallando los signos correspondientes:

KMnO₄ + HCl ⟶ KCl + MnCl₂ + H₂O + Cl₂

K⁺ + MnO₄⁻ + H⁺ + Cl⁻ ⟶ K⁺ + Cl⁻ + Mn²⁺ + 2·Cl⁻ + H⁺ + OH⁻ + Cl₂°

Identificamos los elementos que se reducen y los que se oxidan. Recordar que si un elemento se reduce hay otro que se oxida.

Veamos uno por uno:

K⁺: queda igual de ambos lados del "=" (⟶).

MnO₄⁻: pasa a Mn²⁺, captó 5 electrones, se redujo.

H⁺: queda igual de ambos lados del "=" (⟶), no confundir con el OH⁻.

Cl⁻: pasa a Cl₂°, perdió 1 electrón, se oxidó, pasó a estado gaseoso libre.

Ahora armamos las hemireacciones:

Compensamos el cloro, el hidrógeno y el oxígeno con iones OH⁻:

Ahora equilibramos los electrones, si es necesario, sumando los signos +/- que hay de ambos lados del igual:

Hay que equilibrar los electrones, multiplicando cada hemireacción por el número opuesto de los electrones:

Hacemos cuentas:

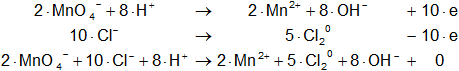
Hemirreacción de oxidación-reducción

Volvemos a la primera ecuación y la armamos con los nuevos coeficientes:

2·KMnO₄ + 10·HCl ⟶ KCl + 2·MnCl₂ + 8·H₂O + 5·Cl₂

Terminamos de equilibrar "a ojo" el K y los H:

2·KMnO₄ + 16·HCl ⟶ 2·KCl + 2·MnCl₂ + 8·H₂O + 5·Cl₂

Debes tomar todo esto como cuentas matemáticas, todo debe quedar igualado.

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo de equilibrar ecuaciones por el método del ion electrón