Problema nº 3 de estequiometría de las soluciones, fracción molar - TP04

Enunciado del ejercicio nº 3

Se tiene una solución formada por 50 g de sulfato de sodio y 50 g de ácido sulfúrico en 500 g de solución, calcular la fracción molar de todos los componentes de la solución.

Desarrollo

Datos:

Soluto 1 = 50 g de Na₂SO₄

Soluto 2 = 50 g de H₂SO₄

Disolvente = 500 g de solución

Solución

Calculamos el peso molecular de los componentes:

Na₂SO₄: 2·23 g + 32 g + 4·16 g = 142 g

H₂SO₄: 2·1 g + 32 g + 4·16 g = 98 g

H₂O: 2·1 g + 16 g = 18 g

La masa del disolvente es:

500 g de solución - 50 g de Na₂SO₄ - 50 g de H₂SO₄ = 400 g de agua

Calculamos cuántos moles hay de cada componente en la solución:

142 g de Na₂SO₄	⟶	1 mol
50 g de Na₂SO₄	⟶	x

x =	50 g de Na₂SO₄·1 mol
	142 g de Na₂SO₄

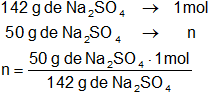
x = 0,352 moles de Na₂SO₄

98 g de H₂SO₄	⟶	1 mol
50 g de H₂SO₄	⟶	x

x =	50 g de H₂SO₄·1 mol
	98 g de H₂SO₄

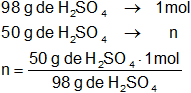
x = 0,510 moles de H₂SO₄

18 g de H₂O	⟶	1 mol
400 g de H₂O	⟶	x

x =	400 g de H₂O·1 mol
	18 g de H₂O

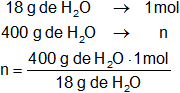
x = 22,222 moles de H₂O

Calculamos la fracción molar del Na₂SO₄:

ƒm =	0,352 moles
	(0,352 + 0,510 + 22,222) moles

Resultado, la fracción molar del Na₂SO₄ es:

ƒm = 0,022

Calculamos la fracción molar del H₂SO₄:

ƒm =	0,510 moles
	(0,352 + 0,510 + 22,222) moles

Resultado, la fracción molar del H₂SO₄ es:

ƒm = 0,015

La fracción molar del H₂O es:

ƒm =	22,222 moles
	(0,352 + 0,035 + 22,222) moles

ƒm = 0,963

Si sumamos las fracciones molares debe resultar "1":

0,022 + 0,015 + 0,963 = 1 ∎

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular la fracción molar de una disolución